Kunci Jawaban
Kunci Jawaban Matematika Kelas 8 Semester 2 Ayo Berlatih 10.3 Halaman 299 300: Peluang
Inilah kunci jawaban matematika kelas 8 semester 2 soal halaman 299 300 bagian Ayo Berlatih 10.3 tentang hubungan Peluang Teoritik dan Peluang Empirik
TRIBUN-BALI.COM – Inilah kunci jawaban matematika kelas 8 semester 2 soal halaman 299 300 bagian Ayo Berlatih 10.3 tentang hubungan Peluang Teoritik dan Peluang Empirik.
Pada kunci Jawaban matematika kelas 8 semester 2 bagian Ayo Berlatih 10.3 halaman 299 300 akan mengulas soal mulai dari nomer 6 hingga 11.
Perlu diketahui, kunci jawaban matematika kelas 8 SMP bagian Ayo Berlatih 10.3 halaman 299 300, telah dibuat sesuai dengan buku matematika kelas 8 semester 2 Kurikulum 2013 edisi revisi 2018.
Setiap kunci jawaban matematika kelas 8 semester 2 pada bagian soal Ayo Berlatih 10.3 halaman 299 300 ini, sudah dilengkapi dengan proses penyelesainnya juga loh.
Itu dilakukan agar para siswa kelas 8 SMP, tidak hanya mengetahui jawabannya saja, tapi juga memahami proses ditemukannya jawaban tersebut.
Baca juga: Kunci Jawaban Matematika Kelas 8 Semester 2 Ayo Berlatih 10.3 Halaman 298 299
Baca juga: Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 291 292, Ayo Berlatih 10.2: Peluang Teoritik
Alangkah baiknya, jika adik-adik kelas 8 SMP mencoba untuk mengerjakan secara mandiri terlebih dahulu, sebelum melihat ke kunci jawaban yang sudah disediakan.
Dilansir dari Tribunnews, berikut adalah kunci jawaban matematika kelas 8 semester 2 Ayo Berlatih 10.3 halaman 299 300 soal nomer 6-11 tentang hubungan Peluang Teoritik dan Peluang Empirik.
Kunci Jawaban Halaman 299-300
Ayo Berlatih 10.3
Soal 6-11
6. Suatu ketika Tohir melakukan percobaan penggelindingan dadu khusus (banyak sisinya belum tentu enam) sebanyak 1.000 kali. Dia hanya mencatat kejadian munculnya mata dadu 1 pada setiap penggelindingan. Beberapa hasilnya disajikan seperti berikut. (pada buku)
a. Menurutmu, berapakah banyak sisi dadu khusus tersebut? Jelaskan.
b. Perkirakan, berapa banyak kali mata dadu 1 muncul pada penggelindingan ke-1.000?
c. Perkirakan, berapa banyak kali Tohir menggelindingkan hingga mencatat kemunculan mata dadu 1 sebanyak 30 kali? Jelaskan.
Jawaban:
Banyak percobaan = 15
Banyak muncul angka 1 = 3
P = n / s
= 3 / 15
= 1/5
a. Banyak sisi dadu khusus tersebut dapat kita lihat dari ruang sampel mata dadu angka "1" (s) / banyak kedaian (n).
= 15/3
= 5
Jadi, banyak sisi dadu khusus tersebut adalah 5.
b. Fh = P(A) x Banyak Percobaan
= 1/5 x 1000
= 200 kali
Jadi, perkiraan banyak muncul mata dadu 1 pada penggelindingan ke-1000 adalah 200 kali.
c. 30 = P(A) x Banyak Percobaan
30 = 1/5 x Banyak Percobaan
Banyak Percobaan = 30 x 5/1
= 150
Jadi, perkiraan banyak tohir menggelindingan hingga muncul angka "1" 30 kali adalah 150 kali.
Baca juga: Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 284, Ayo Berlatih 10.1: Peluang Empirik
7. Nunik melakukan percobaan pemutaran spinner dengan 4 warna yang tidak sama luas. Setelah melakukan percobaan sebanyak 25 kali didapatkan hasil sebagai berikut. (pada buku)
a. Perkirakan bagaimana spinner yang digunakan percobaan oleh Nunik.
b. Jika Nunik melakukan percobaan sebanyak 100 kali, kira-kira berapakali jarum spinner menunjuk ke warna putih? Jelaskan.
Jawaban:
a. Perkiraan spinner yang digunakan:

b. P(putih) = n / s
= 3 / 25
Fh(putih) = P(putih) x banyak percobaan
= 3/25 x 100
= 12
Jadi, kira-kira jarum spinner akan menunjuk warna putih sebanyak 12 kali.
8. Buatlah suatu soal tentang eksperimen dua dadu yang jawabannya adalah peluang kejadian A = 1/2.
Jawaban:
Karena peluang kejadian harus 1/2,
Ruang sampel dadu = 6
Maka banyak kejadian haruslah = 1/2 x 6 = 3
Dadu bernomor 1 hingga 6, maka eksperimen yang cocok adalah kita dapat menggunakan soal:
- Peluang kejadian dadu ganjil atau genap = (1,3,5) atau (2,4,6).
- Peluang kejadian dadu prima atau bukan prima = (2,3,5) atau (1,4,6)
Jadi, soal eksperiman dengan peluang kejadian dadu 1/2 adalah soal tentang peluang Dadu Ganjil/Genap atau peluang Dadu Prima/Bukan Prima.
Baca juga: Ayo Kita Berlatih 6.1, Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 75 76, Lengkap Pembahasan
9. Buatlah suatu soal tentang eksperimen dua dadu yang jawabannya adalah frekuensi harapan kejadian A adalah 1.
Jawaban:
Fh = P(a) x banyak percobaan
Contoh soal:
Tentukan banyak munculnya jumlah dua dadu adalah 12 dari 36 percobaan penggelindingan.
Jumlah dua dadu 12 = (6,6)
n(A) = 1
Ruang sampel 2 dadu = 6 x 6 = 36
s(A) = 36
P(A) = n(A) / s(A)
= 1/36
Fh(A) = P(A) x banyak percobaan
Fh(A) = 1/36 x 46
Fh(A) = 1
Jadi, contoh soalnya adalah "tentukan banyak munculnya jumlah dua dadu adalah 12 dari 36 percobaan".
10. Andaikan kalian adalah manager TIMNAS INDONESIA U-19. Suatu ketika TIMNAS bertanding di Final piala ASIA melawan MALAYSIA. Suatu ketika saat pertandingan sedang berjalan, pada menit ke-89 TIMNAS mendapatkan hadiah PENALTI. Skor sementara adalah 2 – 2. Pemain yang siap menendang adalah EVAN DIMAS, ILHAM, MALDINI, dan MUCHLIS. Seandainya kamu disuruh untuk menentukan penendang penalti tersebut, siapakah yang akan kalian tunjuk agar TIMNAS meraih kemenangan? Berikut catatan tendangan penalti keempat pemain tersebut. (pada buku)
Jawaban:
Peluang Evan Dimas = 16/20
= 4/5
= 80 persen
Peluang Ilham = 14/18
= 7/9
= 77 persen
Peluang Maldini = 12/17
= 70,5 persen
Peluang Muchlis = 11/15
= 73,3 persen
Jadi, yang akan saya tunjuk sebagai penendang penalti agar TIMNAS meraih kemenangan adalah Evan Dimas.
Hal tersebut karena Evan Dimas memiliki peluang yang paling besar dalam memasukan bola ke gawang.
Baca juga: Uji Kompetensi Bab 9, Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 328 329 330 331 332 333
11. Suatu kantong berisi 2 kelereng merah, 3 kelereng putih, dan 5 kelereng biru. Kemudian diambil sebuah kelereng dari kantong itu.
a. Tentukan peluang terambil kelereng merah.
b. Tentukan peluang terambil kelereng putih.
c. Tentukan peluang terambil kelereng bukan biru (biru komplemen).
Jawaban:
ruang sampel = 2 merah, 3 putih, 5 biru
s(a) = 2 + 3 + 5 = 10
a. peluang terambil kelereng merah
P(merah) = n(merah) / s(a)
= 2/10
=1/5
b. peluang terambil kelereng putih
P(putih) = n(putih) / s(a)
= 3/10
c. peluang terambil kelereng bukan biru (biru komplemen)
P(bukan biru) = n(merah) + n(putih)/ s(a)
= (2 + 3) / 10
= 5/10
= 1/2
*) Disclaimer:
- Artikel ini hanya ditujukan kepada orang tua untuk memandu proses belajar anak.
- Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.
Artikel ini telah tayang di Tribunnews.com dengan judul Kunci Jawaban Matematika Kelas 8 Halaman 299 Semester 2, Ayo Kita Berlatih 10.3: Peluang. (*)
kunci jawaban
matematika
semester 2
Kurikulum 2013
Kunci Jawaban Matematika Kelas 8 Halaman 299
Kunci Jawaban Matematika Kelas 8 Halaman 300
Peluang Empirik
Peluang Teoritik
| Kunci Jawaban Matematika Kelas 9 SMP Kurikulum Merdeka Halaman 55, Eksplorasi 2.5 |

|
|---|
| Kunci Jawaban Matematika Kelas 9 SMP Kurikulum Merdeka Halaman 54 55, Ayo Mencoba 2.4 |

|
|---|
| Kunci Jawaban Matematika Kelas 9 SMP Kurikulum Merdeka Halaman 53, Ayo Mencoba 2.3 |

|
|---|
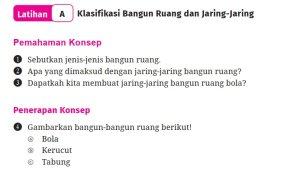
| Kunci Jawaban Matematika Kelas 9 SMP Kurikulum Merdeka Halaman 49, Latihan A |
|
|---|
| Kunci Jawaban Agama Hindu Kelas 8 Semester 1 Kurikulum Merdeka Halaman 31, Ayo Berlatih |

|
|---|










![[FULL] Kirim Pasukan Jadi Gertakan Prabowo ke Israel agar Bebaskan Palestina, Pakar: Gak Omon-omon](https://img.youtube.com/vi/6XEtMFXBdIo/mqdefault.jpg)





Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.