Ayo Kita Berlatih 8.7, Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 200 201 202 Terlengkap

TRIBUN-BALI.COM, DENPASAR – Halo adik-adik, sudah siap belajar? Simak nih, di bawah ini kunci jawaban Matematika kelas 8 semester 2 halaman 200 201 202, ayo kita berlatih 8.7.

Nah adik-adik sekalian, kali ini kita akan membahas soal pada halaman 200 201 202 pada kegiatan siswa ayo kita berlatih 8.7 lengkap dengan kunci jawaban dan pembahasan.

Kunci jawaban matematika kali ini semoga bisa membantu kamu sebagai alternatif jawaban dan membantu kamu dengan penyelesaiannya.

Berikut kunci jawaban dan pembahasan soal Matematika halaman 200 201 202 pada bab ke 8 sesuai dengan buku Matematika kelas 8 kurikulum 2013 edisi revisi tahun 2017.

Baca juga: Ayo Kita Berlatih 8.6, Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 188 189 190 Terlengkap

(Update Kunci Jawaban)

Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 200 201 202

Ayo Kita berlatih 8.7

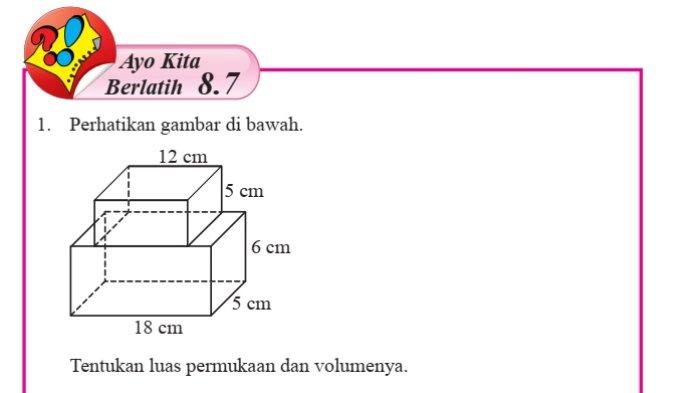
1. Perhatikan gambar di bawah. 

Tentukan luas permukaan dan volumenya.

Jawaban:

Luas permukaan balok I = 2 x ((p x l) + (p x t) + (l x t))

= 2 x ((18 x 5) + (18 x 6) + (5 x 6))

= 2 x (90 + 108 + 30)

= 2 x 228

= 456 cm⊃2;

Baca juga: Ayo Kita Berlatih 8.5, Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 179 180 Terlengkap

Luas permukaan balok II = 2 x ((p x l) + (p x t) + (l x t))

= 2 x ((12 x 5) + (12 x 5) + (5 x 5))

= 2 x (60 + 60 + 25)

= 2 x 145

= 290 cm⊃2;

Luas persegi berhimpit = p x l

= 12 x 5

= 60 cm⊃2;

Luas permukaan seluruhnya = Luas balok I + Luas balok II - (2 x luas berhimpit)

= 456 + 290 - (2 x 60)

= 746 - 120

= 626 cm⊃2;

Volume balok I = p x l x t

= 18 x 6 x 5

= 540 cm⊃3;

Volume balok II = p x l x t

= 12 x 5 x 5

= 300 cm⊃3;

Vbalok seluruhnya = Volume balok I + Volume balok II

= 540 + 300

= 840 cm⊃3;

Jadi, luas permukaannya adalah 626 cm⊃2; dan volumenya adalah 840 cm⊃3;.

Baca juga: Ayo Kita Berlatih 8.4, Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 165 166 167 Terlengkap

2. Perhatikan gambar rangka bangun di samping. 

Rangka bangun tersebut terdiri atas dua bagian, yaitu balok dan limas.

Tentukan:

a. luas permukaan balok.

b. volume balok.

c. luas alas limas.

d. panjang diagonal alas limas.

e. volume limas

Jawaban:

a. Luas permukaan balok = 5 x s x s

= 5 x 8 x 8

= 320 cm⊃2;

b. Volume balok = s x s x s

= 8 x 8 x 8

= 512 cm⊃2;

c. Luas alas limas = panjang EF x panjang FG

= 8 x 8

= 64 cm⊃2;

d. Panjang diagonal alas limas

EG⊃2; = EF⊃2; + FG⊃2;

    = 8⊃2; + 8⊃2;

    = 64 + 64

    = 128

EG = √128

    = 8√2

    = 11,31

Panjang diagonal EG = FH = 11,31 cm⊃2;

e. Volume limas

Volume limas = 1/3 × EF × FG × TO

= 1/3 × 8 cm × 8 cm × 5,65 cm

= 1/3 × 361,6 cm⊃3;

= 120,53 cm⊃3;

3. Sebuah tenda berbentuk bangun seperti berikut. Berapakah luas kain yang digunakan untuk membuat sebuah tenda seperti itu.

Bila alasnya berbentuk persegi dengan ukuran (4 × 4) m⊃2;, tinggi bagian tenda yang berbentuk prisma 2 m dan tinggi sisi tegak bagian atapnya 3 m?

Jawaban:

Luas kain = luas selimut balok + luas sisi tegak pada limas

= (4 x s x t) + (4 x 1/2 x s x tinggi sisi tegak)

= (4 x 4 x 2) + (4 x 1/2 x 4 x 3)

= 32 + 24

= 56

Jadi, luas kain yang digunakan untuk membuat tenda seperti itu adalah 56 m⊃2;.

4. Ambillah enam benda-benda nyata yang ada di sekitar kalian, kemudian ukurlah dan perkirakan luas permukaan dan volumenya.

Jawaban:

- Bangun 1: Akuarium Balok

Panjang = 100 cm, lebar = 30 cm, tinggi = 40 cm

Luas permukaan = 2 x (pl + pt + lt)

= 2 x ((100 x 30) + (100 x 40) + (30 x 40)

= 2 x 8.200

= 16.400 cm⊃2;

Volume = p x l x t

= 100 x 30 x 40

= 120.000 cm⊃3;

- Bangun 2: Toples Tabung

jari - jari = 7 cm, tinggi = 20 cm

Luas permukaan = (2 x luas alas) + (keliling alas x tinggi)

= (2 x pi x r x r ) + (pi x diameter x tinggi)

= (2 x 22/7 x 7 x 7) + (22/7 x 2 x 7 x 20)

= 308 + 880

= 1.188 cm⊃2;

Volume = luas alas x tinggi

= pi x r x r x t

= 22/7 x 7 x 7 x 20

= 3.080 cm⊃3;

- Bangun 3: Penghapus

Panjang = 3 cm, lebar = 1 cm, tinggi = 1 cm

Luas permukaan = 2 x (pl + pt + lt)

= 2 x ((3x1) + (3x1) + (1x1)

= 2 x 7

= 14 cm⊃2;

Volume = p x l x t

= 3 x 1 x 1

= 3 cm⊃3;

- Bangun 4: Sarang Buruk Kubus

Panjang = 30 cm, lebar = 30 cm, tinggi = 30 cm

Luas permukaan = 2 x (pl + pt + lt)

= 2 x ((30 x 30) + (30 x 30) + (30 x 30)

= 2 x 2.700

= 5.400 cm⊃2;

Volume = p x l x t

= 30 x 30 x 30

= 9.000 cm⊃3;

- Bangun 5: Gelas

jari - jari = 3,5 cm, tinggi = 10 cm

Luas permukaan = (2 x luas alas) + (keliling alas x tinggi)

= (2 x pi x r x r ) + (pi x diameter x tinggi)

= (2 x 22/7 x 3,5 x 3,5) + (22/7 x 2 x 3,5 x 10)

= 77 + 220

= 297 cm⊃2;

Volume = luas alas x tinggi

= pi x r x r x t

= 22/7 x 3,5 x 3,5 x 10

= 385 cm⊃3;

- Bangun 6: Balok Kayu

Panjang = 100 cm, lebar = 20 cm, tinggi = 25 cm

Luas permukaan = 2 x (pl + pt + lt)

= 2 x ((100x20) + (100x25) + (20x25)

= 2 x 5.000

= 10.000 cm⊃2;

Volume = p x l x t

= 100 x 20 x 25

= 50.000 cm⊃3;

5. Perhatikan kubus ABCD.EFGH pada gambar berikut.

Titik A, B, C, dan D terletak pada bidang sisi bagian bawah. Titik T merupakan titik perpotongan garis diagonal pada bidang sisi bagian atas. Selanjutnya dibuat limas T.ABCD.

Jika limas T.ABCD dipotong oleh bidang PQRS dimana titik P, Q, R, S, berturut terletak di tengah garis AE, BF, CG, dan DH.

Jika dengan panjang rusuk kubus tersebut adalah 12 cm, maka tentukan volume limas terpancung bagian bawah.

Jawaban:

Panjang rusuk = tinggi limas (TO) = 12 cm

Limas T.ABCD dipotong oleh bidang PQRS dimana titik P, Q, R, S berturut terletak di tengah garis AE, BF, CG, dan DH, maka perbandingan tinggi limas besar dan tinggi limas kecil adalah 2 : 1.

TO : TZ = 2 : 1, sehingga tinggi TZ = 6 cm.

Perhatikan Δ ABT yang sebangun dengan Δ VWT

Karena perbandingan TO : TZ = 2 : 1, maka panjang TW = WB dan TV = VA. dengan perbandingan TB : WB = 2 : 1

Kita bisa menggunakan kesebangunan dalam menentukan panjang VW.

TB : WB = AB : VW

1 : 2 = 12 : VW

1 / 2 = 12 / VW

 VW = 12 / 2

 VW = 6 cm

Jadi, panjang sisi alas VWXY adalah 6 cm.

Untuk menentukan volume limas yang terpancung bagian bawah adalah selisih dari volume limas besar dengan volume kecil.

Volume ABCD.VWXY = Volume T.ABCD - Volume T.VWXY

= (1/3 × AB × BC × TO) - (1/3 × VW × WX × TZ)

= (1/3 × 12 × 12 × 12) cm⊃3; - (1/3 × 6 × 6 × 6) cm⊃3;

= 576 cm⊃3; - 72 cm⊃3;

= 504 cm⊃3;

Jadi, volume limas  terpancung bagian bawah adalah 504 cm⊃3;.

6. Bangunan Candi Borobudur terdiri atas tiga tingkatan, yaitu Kamadhatu, Rupadhatu, dan Arupadhatu.

Arupadhatu merupakan bagian teratas candi yang denah lantainya berbentuk lingkaran.

Di atas lantai ini terdapat sejumlah stupa kecil berbentuk lonceng yang disusun dalam tiga teras lingkaran melingkari stupa induk seperti yang ditunjukkan pada gambar berikut.

Pikirkan berapa banyak stupa kecil pada bagian Arupadhatu tersebut? Tuliskan strategimu.

Jawaban:

Strategi yang dapat dilakukan:

1. Menghitung setengah sisi stupa kecil pada lingkaran terdalam.

2. Mengalikan hasil setengah sisi stupa kecil pada lingkaran terdalam tadi dengan 2.

3. Melakukan langkah 1 dan 2 hingga lingkaran ke-3. Lalu menjumlahkan seluruh stupa kecil pada tiap lingkaran.

- Pada lingkaran pertama terdapat 12 buah

- Pada lingkaran kedua terdapat 24 buah

- Pada lingkaran ketiga terdapat  36 buah

Total stupa kecil = 12 + 24 + 36 = 72 buah

Jadi, banyak stupa kecil pada bagian Arupadhatu tersebut adalah 72 buah.

Demikian kunci jawaban Matematika kelas 8 halaman 200 201 202, kegiatan siswa ayo kita berlatih 8.7 sesuai dengan buku Matematika kurikulum 2013 edisi revisi tahun 2017.

Disclaimer

Kunci jawaban diatas bersifat alternatif jawaban sehingga para siswa bisa memberikan eksplorasi jawaban lain.

Kunci jawaban soal diatas bisa saja berbeda sesuai dengan pemahaman tenaga pengajar atau murid. (*)