Kunci Jawaban
Kunci Jawaban Matematika Kelas 7 Semester 2 Uji Kompetisi 8 Halaman 295 296 297 298
Berikut adalah kunci jawaban matematika kelas 7 SMP semester 2 Uji Kompetensi 8 bagian soal uraian halaman 295, 296, 297, dan 298.
TRIBUN-BALI.COM – Berikut adalah kunci jawaban matematika kelas 7 SMP semester 2 Uji Kompetensi 8 bagian soal uraian halaman 295, 296, 297, dan 298.
Kunci jawaban matematika kelas 7 SMP Uji Kompotensi 8 halaman 295, 296, 297, dan 298 ini, dibuat sesuai buku matematika kelas 7 semester 2 Kurikulum 2013 edisi revisi 2018.
Artikel ini, kita akan membahas soal matematika kelas 7 semester 2 Uji Kompetensi 8 halaman 295, 296, 297, dan 298 bagian uraian, mulai pada nomor 1 hingga 10.
Perlu diketahui, artikel kunci jawaban matematika kelas 7 yang dibagikan kali ini tidak hanya menyediakan seputar jawaban dari soal yang akan dibahas saja, akan tetapi juga menyajikan penjabaran proses pencarian jawaban tersebut.
Hal tersebut dilakukan agar para siswa kelas 7 SMP, tidak hanya mengetahui jawabannya saja, tapi juga memahami proses ditemukannya jawaban tersebut.
Baca juga: Kunci Jawaban Matematika Kelas 7 Semester 2 Uji Kompetisi 8 Halaman 292 293 294
Baca juga: Kunci Jawaban Matematika Kelas 7 Semester 2 Uji Kompetensi 8 Halaman 289 290 291
Dilansir dari Tribunnews, berikut kunci jawaban matematika kelas 7 SMP semester 2 Uji Kompetensi 8 halaman 295, 296, 297, dan 298 bagian uraian, dimulai pada nomor 1 hingga 10.
Kunci Jawaban 295 296 297 298
Uji Kompetensi 8
B. Soal Uraian
1. Misalkan suatu persegi diletakkan berimpit di kanan persegi yang lainnya. Tentukan keliling persegi yang terdiri dari:
a. 1 persegi
b. Gabungan 2 persegi
c. Gabungan 3 persegi
d. Gabungan n persegi
e. Berikan alasan yang digunakan untuk menggeneralisasi soal butir d.
Jawaban:
a. 4a
b. 6a
c. 8a
d. (2n + 2)a
e. Dengan memperhatikan pola mulai keliling 1 persegi, 2 persegi, 3 persegi, dan seterusnya. Membentuk pola bilangan genap yang dimulai dari bilangan 4, sehingga didapat untuk sebanyak n persegi = (2n + 2)a
2. Misalkan a merupakan alas jajar genjang PQRS dengan t merupakan tingginya.
Jika 2t = 3a, tentukan:
a. panjang t dalam a.
b. panjang alas dan tingginya jika luas jajar genjang tersebut 864 cm2.
Jawaban:
a. 2t = 3a
t = 3a/2
b. a x t = 864 cm²
a x 3a/2= 864 cm²
a² = 864 x 2/3
a = √576
= 24 cm
Baca juga: Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 282 283: Memahami Garis Istimewa Segitiga
3. Diketahui keliling ∆KLM adalah 40 cm.
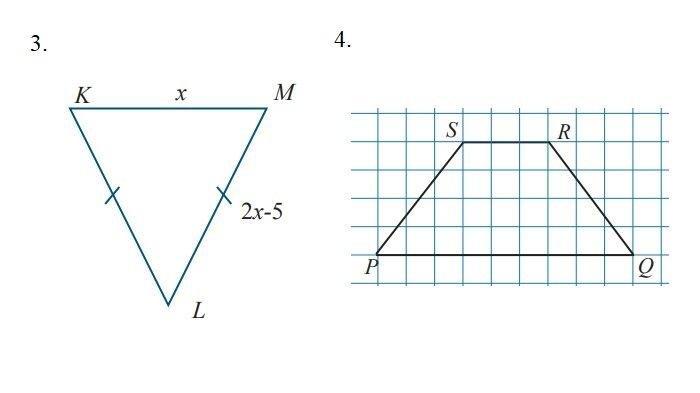
a. Berbentuk apakah ∆KLM ?
b. Tentukan panjang sisi ∆KLM !
Jawaban:
a. Segitiga AKM merupakan segitiga sama kaki.
b. Tentukan panjang sisi ∆KLM !
Keliling = ML + KL + KM
40 = x + 2x-5 + 2x-5
40 = 5x -10
5x = 40 + 10
5x = 50
x = 50 :5
x = 10
Maka panjang KM = x = 10 cm ; ML dan KL = 2x-5 = 2(10) - 5 = 20 - 5 = 15 cm
4. Keliling segi-4 PQRS pada gambar di bawah adalah 22 cm.
a. Tentukan panjang PQ, SR, PS dan RQ!
b. Bagaimanakah caramu menghitung luas PQRS?
c. Berapakah luas PQRS?
Jawaban:
a. Berdasarkan kotak kecil yang panjangnya 1cm, maka :
PQ = 9 cm
SR = 3 cm
SP + RQ = 22 - PQ - SR
= 22 - 9 - 3
= 10
Karena SP sama dengan RQ maka masing, masing adalah 5cm,
SP = 5 cm
RQ = 5 cm
b. Cara menghitung luas PQRS menggunakan rumus luas trapesium,
Luas trapesium PQRS = 1/2 x jumlah sisi sejajar x tinggi
c. Luas = 1/2 x (PQ + SR) x t
= 1/2 x (9 + 3) x t
= 24 cm2
Baca juga: Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 272 273: Hitung Keliling dan Luas Segitiga
5. Diketahui bangun-bangun seperti berikut.
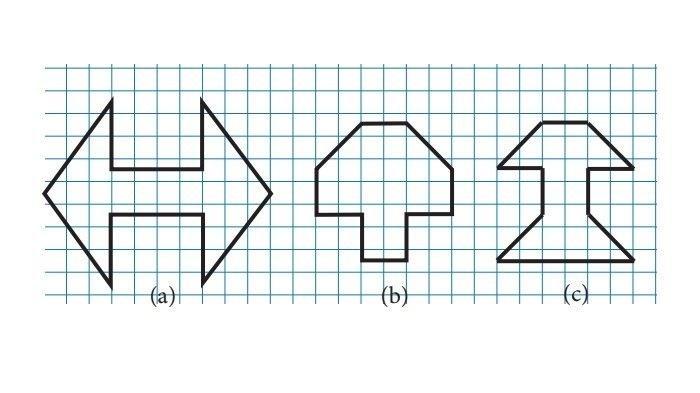
a. Tentukan luas dari tiap-tiap bangun di atas.
b. Bangun manakah yang mempunyai luas terbesar?
Jawaban:
a. Luas bangun (a) = (2 x luas segitiga) + luas persegi panjang
= (2 x 1/2 x a x t) + (p x l)
= (2 x 1/2 x 8 x 3) + (4 x 2)
= 24 + 8
= 32 satuan luas
Luas bangun (b) = (2 x luas trapesium) + luas persegi panjang
= (2 x 1/2 x (a+b) x t) + (p x l)
= (2 x 1/2 x (2 + 4) x 2) + (6 x 2)
= 12 + 12
= 24 satuan luas
Luas bangun (c) = (2 x luas trapesium) + luas persegi
= (2 x 1/2 x (a + b) x t) + (s x s)
= (2 x 1/2 x (2 + 6) x 2) + (2 x 2)
= 16 + 4
= 20 satuan luas
b. Bangun yang memiliki luas terbesar adalah bangun (a) dengan total luas 32 satuan luas.
6. Perhatikan gambar berikut.
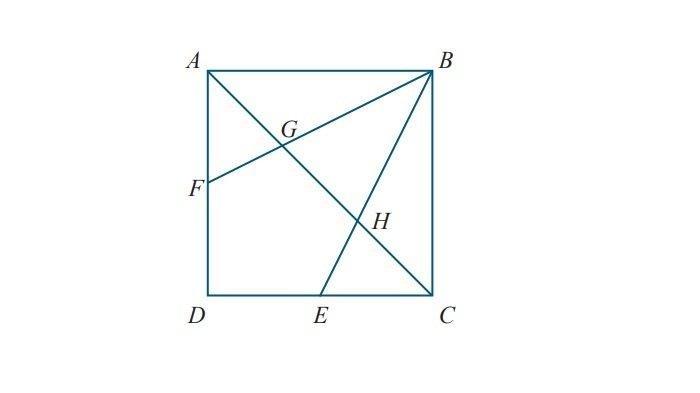
ABCD persegi dengan panjang sisi-sisinya adalah 2 cm. E adalah titik tengah CD dan F adalah titik tengah AD. Luas daerah EDFGH adalah ... cm2.
Jawaban:
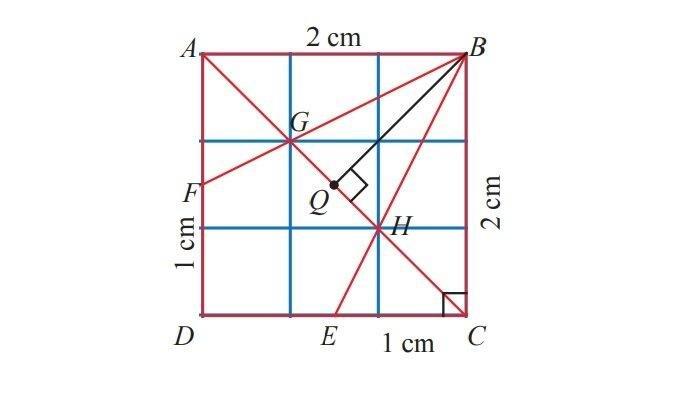
Luas daerah EDFGH = Luas persegi ABCD – (2 x Luas BCE) – Luas ΔBHG.
= 4/3 cm2
Jadi, luas EDFGH adalah 4/3 cm2.
Baca juga: Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 270 271: Hitung Keliling dan Luas Segitiga
7. Perhatikan gambar di bawah. Terdapat 4 buah layang-layang kongruen yang termuat pada persegi dan ternyata masih tersisa daerah persegi yang diarsir. Jika panjang p = 3 2 cm, dan q = 5 2 cm, maka luas daerah yang diarsir adalah …. cm2 (OSP SMP 2009)
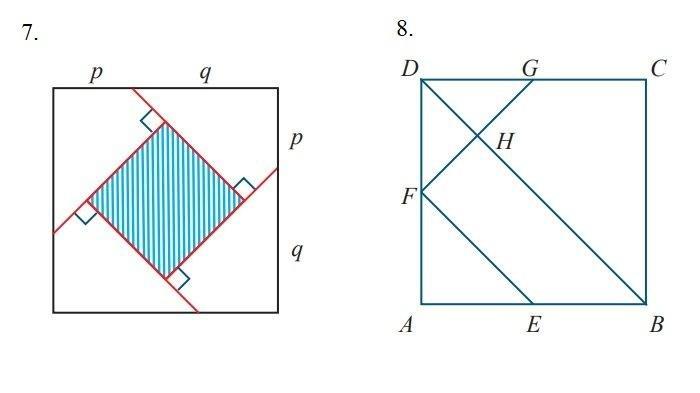
Jawaban:
Carilah panjang p + q, luas persegi besar, luas segitiga ABC
Luas daerah yang diarsir = Luas persegi – 8 Luas segitiga ABC
Jadi, luas daerah yang diarsir adalah 8 cm2.
8. Diketahui luas persegi ABCD adalah 25 m2. Jika E, F, dan G masingmasing adalah titik tengah AB, AD, dan CD seperti pada gambar berikut, maka luas trapesium BHFE adalah .... m2.
(OSP SMP 2011)
Jawaban:
Carilah panjang AE, BE, AF, FD, DG, dan GC, selanjutnya dapatkan luas trapesium BHFE:
Luas Trapesium BHFE = Luas ΔABD – Luas ΔAEF – Luas ΔDFH Jadi, luas daerah yang diarsir adalah 7,8125 cm2.
9. PATIO/ Ember terbuka di belakang rumah Nick ingin membuat patio terbuka di belakang rumah barunya. Panjang Patio adalah 5, 25 meter dan lebarnya 3 meter. Ia memerlukan 81 buah batu bata per m2.
Hitunglah berapa banyak batu bata yang diperlukan Nick untuk membuat pationya itu!
Jawaban:
Luas Patio = p x l
= 5,25 x 3
= 15,75 m2
Banyak batu = Luas / 1 x 81
= 15,75 /1 x 81
= 1275,75 batu
Jadi, banyak batu bata yang diperlukan untuk membuat patio adalah 1275,75 batu bata.
Baca juga: Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 254 255 256 257: Jenis dan Sifat Segitiga
10. Perhatikan gambar sebuah jajargenjang berikut
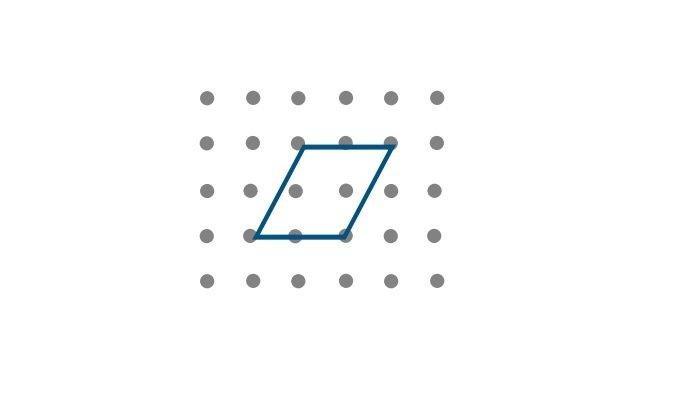
Pada kotak jawaban, buatlah minimal 4 segiempat lain yang berbeda dan memiliki luas yang sama dengan luas jajargenjang yang ditunjukkan pada gambar di atas.
(Catatan: Dua segiempat atau lebih disebut sama jika segiempat yang satu merupakan hasil pencerminan atau perputaran bangun yang lain)
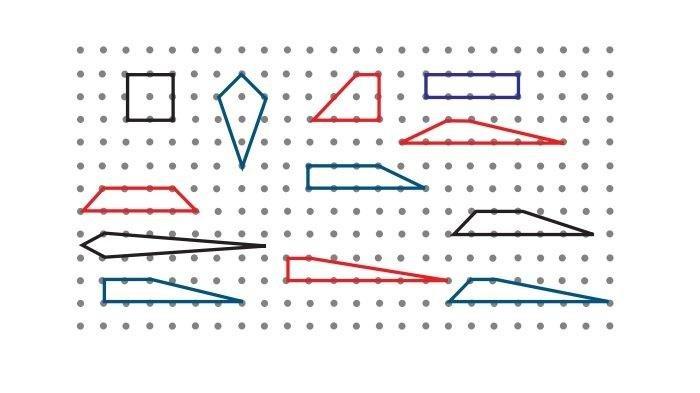
Jawaban:
Luas jajar genjang tersebut adalah, 4 satuan luas. Oleh karena itu kita mencari bangun lain yang memiliki luas yang sama dengan jajargenjang tersebut.
*) Disclaimer:
- Artikel ini hanya ditujukan kepada orang tua untuk memandu proses belajar anak.
- Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa. (*)
Artikel ini telah tayang di Tribunnews.com dengan judul Kunci Jawaban Matematika Kelas 7 Halaman 295 296, Uji Kompetensi 8: Soal Uraian dan Kunci Jawaban Matematika Kelas 7 Halaman 297 dan 298 Semester 2, Uji Kompetensi 8: Soal Uraian.
kunci jawaban
matematika
semester 2
Kurikulum 2013
Uji Kompetensi 8
Kunci Jawaban Matematika Kelas 7 Halaman 295
Kunci Jawaban Matematika Kelas 7 Halaman 296
Kunci Jawaban Matematika Kelas 7 Halaman 297
Kunci Jawaban Matematika Kelas 7 Halaman 298
| Jawaban Eksplorasi 1.3, Kunci Jawaban Matematika Kelas 5 Halaman 15 16 Kurikulum Merdeka |

|
|---|
| Jawaban Ayo Berlatih, Kunci Jawaban Matematika Kelas 5 Halaman 14 15 Kurikulum Merdeka |

|
|---|
| Jawaban Ayo Berlatih, Kunci Jawaban Matematika Kelas 5 Halaman 8 9 Kurikulum Merdeka |

|
|---|
| Jawaban Ayo Berpikir Kritis, Kunci Jawaban Matematika Kelas 5 Halaman 7 Kurikulum Merdeka |

|
|---|
| Kunci Jawaban Agama Hindu Kelas 8 Halaman 57 Kurikulum Merdeka, Asesmen Bab 2 |

|
|---|















Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.