Kunci Jawaban Matematika Kelas 7 Semester 1 Halaman 163, Ayo Kita Menalar: Komplemen Himpunan

TRIBUN-BALI.COM, DENPASAR – Apa kalian sudah siap? Simak nih, berikut ini kunci jawaban Matematika Kelas 7 Semester 1 halaman 163, Ayo Kita Menalar: Komplemen Himpunan.

Kali ini kita akan membahas soal pada bab ke 2 yang berjudul Himpunan pada kegiatan siswa Ayo Kita Menalar tentang Komplemen Himpunan.

Kunci jawaban di bawah ini diharapkan bisa membantu siswa sebagai alternatif jawaban untuk menyelesaikan soal pada halaman 163 di buku siswa Matematika Kelas 7.

Berikut kunci jawaban dan pembahasan soal Matematika Kelas 7 Semester 1 halaman 163 sesuai dengan buku Matematika Kurikulum 2013 edisi revisi tahun 2017.

Baca juga: Kunci Jawaban Matematika Kelas 11 Halaman 14 15 16 17 18, Latihan: Bentuk Bilangan dalam Polar

(Update Kunci Jawaban)

Kunci Jawaban Matematika Kelas 7 Semester 1 Halaman 163

Ayo Kita Menalar

1. Misalkan A dan B adalah himpunan, selidiki apakah

a. (A ∪ B)c = Ac ∩ Bc

b. (A ∩ B)c = Ac ∪ Bc

c. (Ac)c = A

Baca juga: Kunci Jawaban Matematika Kelas 11 Halaman 19 20 23 24, Kurikulum Merdeka: Tentukan Jarak Pengereman

2. Hasil survey tentang acara televisi yang paling disukai warga yang usianya di atas 17 tahun di RT 05 kelurahan Arjosari adalah 110 warga suka sinetron.

90 warga suka olah raga, 20 orang suka keduanya, dan 5 orang tidak suka keduanya.

a. Gambarlah diagram Venn dari keterangan tersebut

b. Berapa banyak warga RT 05 kelurahan Arjosari?

c. Berapa banyak warga yang tidak suka pada acara sinetron?

d. Berapa banyak warga yang tidak suka pada acara olahraga?

Baca juga: Kunci Jawaban Matematika Kelas 8 Semester 1 Halaman 127 128 129 130, Uji Kompetensi Bab 3

Jawaban:

Soal nomor 1

Misalkan A dan B adalah himpunan,

a. Untuk membuktikan apakah (A ∪ B)^c = A^c ∩ B^c

Coba perhatikan diagram Venn berikut ini

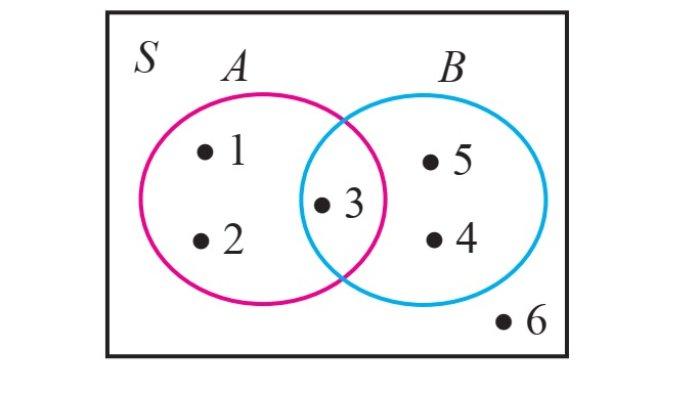
Dari diagram Venn tersebut diperoleh bahwa

(A ∪ B) = {1, 3, 5, 7} dan A^c = {4, 5, 6}

B^c = {1, 2, 6}

(A ∪ B)^c = {6} A^c ∩ B^c = {6}

Ternyata (A ∪ B)^c = {6} dan A^c ∩ B^c = {6}, sehingga terbukti bahwa (A ∪ B)^c = A^c ∩ B^c

b. Untuk membuktikan apakah (A ∩ B)^c = A^c ∪ B^c

Coba perhatikan diagram Venn berikut ini

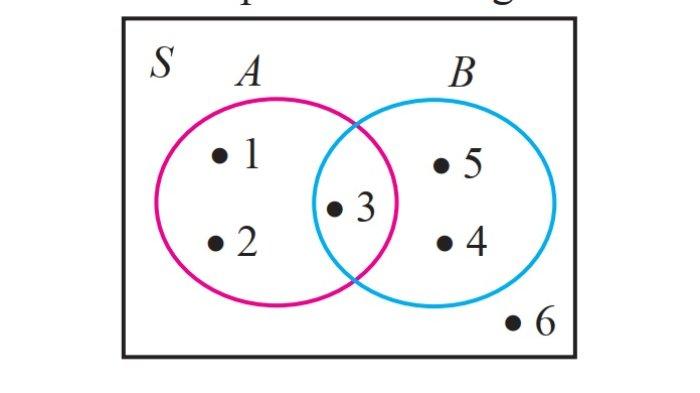
Dari diagram Venn tersebut diperoleh bahwa

(A ∩ B) = {3} dan A^c = {4, 5, 6}

B^c = {1, 2, 6}

(A ∩ B)^c = {1, 2, 4, 5, 6} A^c ∪ B^c = {1, 2, 4, 5, 6}

Ternyata (A ∩ B)^c = {1, 2, 4, 5, 6} dan A^c ∪ B^c = {1, 2, 4, 5, 6}, sehingga terbukti bahwa (A ∩ B)^c = A^c ∪ B^c

c. Untuk membuktikan bahwa (Ac)^c = A

Perhatikan kembali diagram Venn diatas

A = {1, 2, 3}

Ac = {4, 5, 6}

(Ac)c = {1, 2, 3}

Ternyata (A^c)^c = A

Soal nomor 2

Hasil survey tentang acara televisi yang paling disukai warga yang usianya diatas 17 tahun di RT 05 kelurahan Arjosari adalah 110 warga suka sinetron.

90 warga suka olah raga, 20 orang suka keduanya, dan 5 orang tidak suka keduanya.

Misalkan A adalah himpunan warga yang suka sinetron.

B adalah himpunan warga yang suka olah raga.

a. Gambar diagram Venn dari keterangan tersebut adalah:

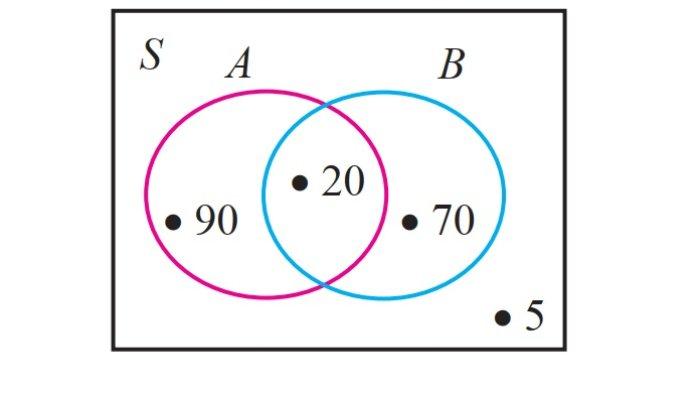
b. Banyak warga RT 05 kelurahan Arjosari adalah

90 + 20 + 70 + 5 = 185

c. Banyak warga yang tidak suka pada acara sinetron adalah 70 orang

d. Banyak warga yang tidak suka pada acara olah raga 90 orang

Keterangan (^) berarti pangkat

Demikian kunci jawaban Matematika Kelas 7 Semester 1 halaman 163, soal kegiatan siswa Ayo Kita Menalar: Komplemen Himpunan sesuai dengan Kurikulum 2013 edisi revisi tahun 2017.

Disclaimer

Kunci jawaban diatas bersifat alternatif jawaban sehingga para siswa bisa memberikan eksplorasi jawaban lain.

Kunci jawaban soal diatas bisa saja berbeda sesuai dengan pemahaman tenaga pengajar atau murid. (*)