Kunci Jawaban
Kunci Jawaban Matematika Kelas 12 Halaman 25 26, BAB 1: Menghitung Panjang Rusuk Kubus
Berikut kunci Jawaban dan pembahasan soal mapel matematika kelas 12 SMA halaman 25 26 BAB 1.
TRIBUN-BALI.COM, DENPASAR - Berikut kunci Jawaban dan pembahasan soal mapel matematika kelas 12 SMA halaman 25 26 BAB 1.
Kunci Jawaban Matematika Kelas 12 Halaman 25
Kunci Jawaban Matematika Kelas 12 Halaman 26
Artikel ini akan memudahkanmu dalam mengerjakan soal-soal matematika.
Mengerjakan soal matematika SMA tak sulit lagi dengan ulasan ini.
Baca juga: Kunci Jawaban PKN Kelas 10 Halaman 65 66, Kurikulum Merdeka: Identfikasi Tugas dan Fungsi Lembaga
Berikut kunci jawabannya yang berhasil dirangkum TribunBali.com dari berbagai sumber.
Pada bagian ini, siswa diminta untuk mengerjakan soal bagian BAB 1, Dimensi Tiga.
Simak selengkapnya di sini.
Kunci Jawaban Matematika Kelas 11 Halaman 25 26
Soal Halaman 25
Bab 1 buku ini berjudul “Dimensi Tiga”.
Jawablah pertanyaan berikut disertai dengan langkah pengerjaannya!
Kunci Jawaban Matematika Kelas 11 Halaman 25
1. Perhatikan gambar berikut.
a. Dari Gambar (a), tentukan jarak dari titik A ke D.
b. Dari Gambar (b), tentukan jarak titik P terhadap garis g.
c. Dari Gambar (c), tentukan jarak titik P pada bidang-K.
Alternatif Penyelesaian:
a. Jarak titik A ke D = 46 m.
b. Jarak titik P terhadap garis g adalah panjang ruas garis PP1
c. Jarak titik P ke bidang K adalah panjang ruas garis PP1
Kunci Jawaban Matematika Kelas 11 Halaman 25 Nomor 1 (Banjarmasin Post)
2. Diketahui kubus ABCD.EFGH dengan panjang rusuk 9 cm. Buat ilustrasi kubus tersebut. Tentukan langkah menentukan jarak titik F ke bidang BEG. Kemudian hitunglah jarak titik F ke bidang BEG.
Alternatif Penyelesaian:
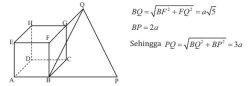
3. Diketahui kubus ABCD.EFGH dengan panjang rusuk a. Jika titik P terletak pada perpanjangan AB sehingga PB = 2a, dan titik Q pada perpanjangan FG sehingga QG = a.
a. Buatlah ilustrasi dari masalah di atas.
b. Tentukan PQ.
Alternatif Penyelesaian:
Baca juga: Kunci Jawaban Fisika Kelas 11 Halaman 55 60 61, Kurikulum Merdeka: Menghitung Jarak Tempuh Benda
4. Panjang setiap bidang empat beraturan T.ABC sama dengan 16 cm. Jika P pertengahan AT dan Q pertengahan BC, tentukan PQ.
Alternatif Penyelesaian:
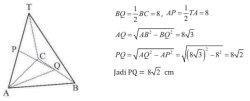
5. Perhatikan gambar kubus ABCD.EFGH. Tentukan jarak titik H ke DF.
Alternatif Penyelesaian:

6. Dalam kubus ABCD.EFGH titik S adalah titik tengah sisi CD dan P adalah titik tengah diagonal ruang BH. Tentukan perbandingan volum limas P.BCS dan volum kubus ABCD.EFGH.
Alternatif Penyelesaian:
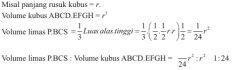
7. Diketahui kubus ABCD.EFGH dengan panjang rusuk a cm. S merupakan proyeksi titik C pada bidang AFH.Tentukan jarak titik A ke titik S.
Alternatif Penyelesaian:
8. Diketahui kubus ABCD.EFGH dengan panjang rusuk cm. P dan Q masing- masing merupakan titik tengah AB dan CD, sedangkan R merupakan titik potong EG dan FH. Tentukan jarak titik R ke bidang EPQH.
9. Diketahui kubus ABCD.EFGH dengan rusuk 4 cm. P titik tengah EH. Tentukan jarak titik P ke garis CF.
Baca juga: Kunci Jawaban Matematika Kelas 12 Halaman 54 55, Tugas: Kesalahan Masing-Masing Distribusi Frekuensi
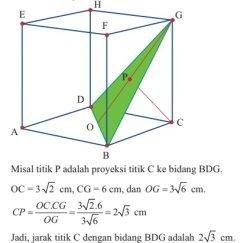
10. Panjang rusuk kubus ABCD.EFGH adalah 6 cm. Tentukan jarak titik C dengan bidang BDG.
Alternatif Penyelesaian:
Kunci Jawaban Matematika Kelas 12 Halaman 26
6. Dalam kubus ABCD.EFGH titik S adalah titik tengah sisi CD dan P adalah titik tengah diagonal ruang BH. Tentukan perbandingan volum limas P.BCS dan volum kubus ABCD.EFGH.
Jawaban:
Cari terlebih dahulu volume limas P.BCS
Volume limas P.BCS:
= 1/3 x Luas alas x t
= 1/3 x 1/2 x BC x SC x 1/2a
= 1/3 x 1/2 x a x 12a x 1/2a
= 1/24a3
Cari volume kubus ABCD.EFGH
Diketahui perbandingan volume limas P.BCS dan volume kubus ABCD.EFGH adalah:
= 1/24a3 : a3
= 1/24 : 1
= 1 : 24
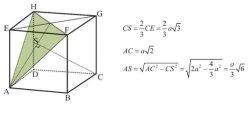
7. Diketahui kubus ABCD.EFGH dengan panjang rusuk a cm. S merupakan proyeksi titik C pada bidang AFH.Tentukan jarak titik A ke titik S.
Jawaban:
Diketahui dari segitiga ACP maka:
AP = CP = 1/2 a√6 (diperoleh phytagoras AE dan EP)
AC = a√2 (diagonal sisi)
PQ = a (rusuk kubus)
Dengan saling tegak lurus, maka berlaku aturan luas pada segitiga yakni:
AC x PQ = AP x CS
CS = AC x PQ/AP
CS = a√2 x a / (1/2a√6)
CS = 2a√2 /√6
CS = 2a/√3
CS = 2/3 a√3
Dan juga berlaku phytagoras sebagai berikut:
AS2 = AC2 -CS2
AS2 = (a√2)2 - (2/3 a√3)2
AS2 = 2a2 - 4/3a2
AS2 = 2/3 a2
AS = √(2/3a2)
AS = a√2 / √3
Dengan rasionalisasi:
AS = 1/3 a√6 cm
Baca juga: Kunci Jawaban Fisika Kelas 11 Halaman 65 66 67 68 70, Latihan 2.2: Panjang Garis Singgung
8. Diketahui kubus ABCD.EFGH dengan panjang rusuk cm. P dan Q masing-masing merupakan titik tengah AB dan CD, sedangkan R merupakan titik potong EG dan FH. Tentukan jarak titik R ke bidang EPQH.
Jawaban:
Buat titik bantu S yang terletak di tengah garis EH
Buat titik bantu T yang terletak di tengan garis PQ
Hubungkan titik R ke titik S dan titik R ke titik T seningga membentuk segitiga
SRT Siku-Siku di R.
Titik R merupakan titik potong EG dan FH, sehingga:
RS = 1/2 x GH
RS = 1/2 x a
RS = 1/2a cm
RT = rusuk kubus
RT = a cm
Lihat segitiga SRT siku-siku di R. Cari besarnya TS dengan teorema Phytagoras, didapatkan:
TS = √(RS2 +RT2)
TS = √(1/2a2 + a2)
TS = a√(1/4 + 1)
TS = a√5/4
TS = a√1/4 x √5
TS = 1/2 a√5 cm
Buat titik bantu O yang terletak di tengan garis ST.
RO merupakan jarak titik R ke bidang EPQH.
Dengan perbandingan segitiga SRT, maka didapatkan:
RS x RT=TS x RO
1/2a x a= 1/2a√5 x RO
RO = 1/2a x a / 1/2a√5
RO = 1/5 a √5 cm
Jadi, jarak titik R ke bidang EPQH adalah 1/5 a √5 cm
9. Diketahui kubus ABCD.EFGH dengan rusuk 4 cm. P titik tengah EH. Tentukan jarak titik P ke garis CF.
Jawaban:
P titik tengah EH, maka
Untuk mencari jarak titik P ke CF, buat segitiga PCF dengan ukuran-ukuran sisinya adalah:
Panjang CF
CF = √(FB2 + BC2)
CF = √(42 +42)
CF = √(16 + 16)
CF = √32
CF = √(16 x 2)
CF = 4√2 cm
Atau sebenarnya bisa langsung saja karena pada kubus dengan rusuk s, memiliki panjang
Diagonal sisi = s√2
Diagonal ruang = s√3
sehingga
Panjang CF = 4√2 cm CF adalah diagonal sisi kubus
Panjang PF
PF = √(FE2 + EP2)
PF = √(42 +22)
PF = √(16 + 4)
PF = √20
PF = √(4x5)
PF = 2√5 cm
Panjang PC
HC adalah diagonal Sisi kubus, maka HC = 4√2 cm
PC = √(PH2 + HC2)
PC = √(22 + (4√2)2)
PC = √(4 + 32)
PC = √36
PC = 6 cm
Jadi segitiga PCF adalan segitiga sembarang.
Jarak titik P ke garis CF adalan PQ dengan PQ adalah tinggi segitiga PCF yang alasnya di sisi CF
Dengan menggunakan aturan kosinus, kita akan mencari nilai kosinus sudut F, yakni:
PC2 = PF2 + CF2 - 2 x PF x CF x cos F
62 = (2√5)2 + (4v2)2 - 2 x 2√5 x 4√2 x cos F
36 = 20 + 32 - 16√10 cos F
16√10 cos F = 20 + 32 - 36
16√10 cos F = 16
cos F = 16/16√10
cos F = 1/√10
cos F = sa/mi
Sisi samping (sa) = 1
Sisi miring (mi) = √10
maka sisi depan (de) adalah:
de = √((√10)2 -12)
de = √(10-1)
de = √9
de = 3
Sehingga nilai dari F adalah
sin F = de/mi
sin F = 3/√10
Sisi depan sudut F : de = PQ
Sisi miring : de = PF = 2√5 cm

10. Panjang rusuk kubus ABCD.EFGH adalah 6 cm. Tentukan jarak titik C dengan bidang BDG.
Jawaban:
Jarak titik C ke BDG = jarak titik C ke garis GO = tinggi segitiga CGO dengan GO (O adalah titik tengah BD)
CG = 6 cm (rusuk kubus)
OC = 1/2AC = 1/2(6√2 cm) = 3√2 cm (AC adalah diagonal sisi)
GO = √(CG2 + OC2)
GO = √(62 + (3√2)2)
GO = √(36 + 18)
GO = √(54)
GO = √(9.6)
GO = 3√6
Pada segitiga CGO
Jika alasnya OC maka tingginya CG
Jika alasnya GO maka tingginya adalah jarak titik C ke BDG
Dengan kesamaan luas segitiga (1/2 x alas x tinggi), maka diperoleh:
1/2 x GO x t = 1/2 x OC x CG
GO x t = OC x CG
3√6 x t = 3√2 x 6
t = (3√ x 6) / 3√6
t = 6 / √3
t = (6 / √3) x (√3/√3)
t = 6√3 / 3
t = 2 √3
Disclaimer:
Itu dia kunci jawaban dan soal ulasan matematika kelas 12.
Pembahasan dan kunci jawaban ini hanya digunakan sebagai panduan belajar siswa.
Siswa diharapkan untuk mengerjakan soal terlebih dahulu secara mandiri.
Kunci Jawaban Matematika Kelas 12 Halaman 25
Kunci Jawaban Matematika Kelas 12 Halaman 26
kunci
Jawaban
pembahasan soal
matematika
kelas 12
| Kunci Jawaban Matematika Kelas 9 SMP Kurikulum Merdeka Halaman 34 35 36, Uji Kompetensi Bab 1 |

|
|---|
| Kunci Jawaban Matematika Kelas 9 SMP Kurikulum Merdeka Halaman 33 34, Uji Kompetensi Bab 1 |

|
|---|
| Kunci Jawaban Matematika Kelas 9 SMP Kurikulum Merdeka Halaman 29 30 31, Latihan B |

|
|---|
| Kunci Jawaban Matematika Kelas 9 SMP Kurikulum Merdeka Halaman 28, Ayo Berpikir Kritis 1.4 |

|
|---|
| Kunci Jawaban Agama Hindu Kelas 7 Semester 2 Kurikulum Merdeka Halaman 146 147 148, Asesmen Bab 5 |

|
|---|










![[FULL] Bongkar Pasang Kabinet Prabowo Kursi BUMN Kini Kosong, Pakar: Rosan Roeslani Opsi Terbaik](https://img.youtube.com/vi/80Tee_6ti7Q/mqdefault.jpg)





Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.