Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 93 94, Ayo Kita Berlatih 7.3: Soal Essai 1-9

Pb = 1.256 cm

π = 3,14

Ditanya: r…?

Jawab: Pb = α/360 x 2πr

1.256 = 72/360 x 2 x 3,14 x r

1.256 = 1/5 x 6,28 x r

r = (1.256 x 5)/6,28

r = 6.280/6,28

r = 1.000 cm

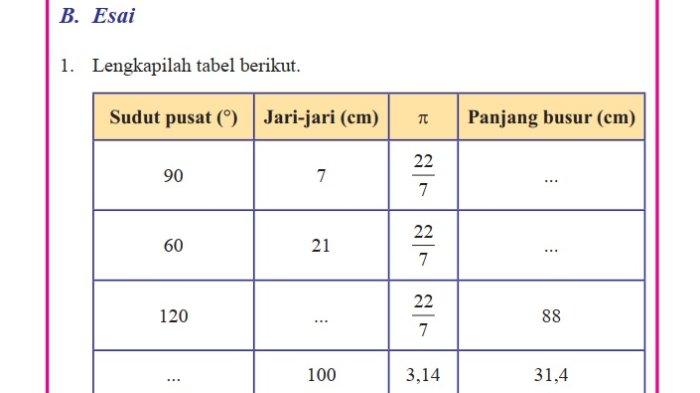
2. Lengkapilah tabel berikut.

- Diketahui: α = 100°

r = 6 cm

π = 3,14

Ditanya: Luas juring (Lj)…?

Jawab: Lj = α/360 x πr⊃2;

Lj = 100/360 x 3,14 x 6 x 6

Lj = 11.304/360

Lj = 31,4

- Diketahui: α = 25°

Lj = 31,4 cm

π = 3,14

Ditanya: r…?

Jawab: Lj = α/360 x πr⊃2;

31,4 = 25/360 x 3,14 x r⊃2;

r⊃2; = (31,4 x 360)/(25 x 3,14)

r⊃2; = 11.304/78,5

r⊃2; = 144

r = 12

- Diketahui: Lj = 8.478

r = 90 cm

π = 3,14

Ditanya: α …?

Jawab:

Lj = α/360 x πr⊃2;

8.478 = α/360 x 3,14 x (90)⊃2;

8.478 = α/360 x 3,14 x 8.100

α = (8.478 x 360)/(3,14 x 8.100)

α = 3.052.080/25.434

α = 120°

3. Tentukan luas juring lingkaran yang diketahui sudut pusatnya 70° dan jari-jarinya 10 cm.

Jawaban:

Karena r = 10 cm gunakan nilai π = 3,14

L juring = sudut pusat/360° x πr⊃2;

= 70/360 x 3,14 x 10⊃2;

= 7/36 x 3,14 x 100

= 7/36 x 314

= 2.198/36

= 61,055

Jadi, luas juring lingkaran tersebut adalah 61,055 cm⊃2;.

4. Tentukan panjang busur lingkaran yang diketahui sudut pusatnya 35° dan jari-jarinya 7 cm.

Jawaban:

Karena r = 7 cm (kelipatan 7 maka gunakan nilai π = 22/7

Panjang busur = sudut pusat / 360° x 2πr

= 35/360 x 2 x 22/7 x 7

= 35/360 x 2 x 22

= 35/360 x 44

= 1.540/360

= 4,277

Jadi, panjang busur lingkaran tersebut adalah 4,277 cm.

5. Lingkaran A memiliki jari-jari 14 cm. Tentukan sudut pusat dan jari-jari suatu juring lingkaran lain agar memiliki luas yang sama dengan lingkaran A.

Jawaban:

Luas lingkaran A = πr⊃2; 

= π × (14 cm)⊃2; 

= 196π cm⊃2;

Misal sudut pusat juring lingkaran yang lain adalah α dan jari-jari R, maka

Luas juring = luas lingkaran A

α/360 × πR⊃2; = 196π

α/360 × R⊃2; = 196

α × R⊃2; = 360⁰ × 196

α × R⊃2; = 360⁰ × 14⊃2;

- Kemungkinan pertama:

α × R⊃2; 

= 360⁰ × 14⊃2; 

= 90⁰ × 4 × 14⊃2;

= 90⁰ × 2⊃2; × 14⊃2;

= 90⁰ × (2 × 14)⊃2;

= 90⁰ × 28⊃2;

Jadi α = 90⁰ dan R = 28 cm

- Kemungkinan kedua:

α × R⊃2; 

= 360⁰ × 14⊃2; 

= 40⁰ × 9 × 14⊃2;

= 40⁰ × 3⊃2; × 14⊃2;

= 40⁰ × (3 × 14)⊃2;

= 40⁰ × 42⊃2;

Jadi α = 40⁰ dan R = 42 cm

6. Buatlah lingkaran A dengan jari-jari tertentu, sedemikian sehingga luasnya sama dengan juring pada lingkaran B dengan sudut pusat dan jari-jari tertentu. Jelaskan.

Jawaban:

Misal jari-jari = 21 cm dan sudut pusat 160° untuk juring B

L = 160/360 x 22/7 x 21 x21

= 616

616 = 22/7 x r⊃2;

r⊃2; = 4312/22

r⊃2; = 196

r = 14

Jadi, jari-jari lingkaran A adalah 14 cm.

7. Diketahui: (1) lingkaran penuh dengan jari-jari r, (2) setengah lingkaran dengan jari-jari 2r. Tentukan manakah yang kelilingnya lebih besar?

Jawaban:

(1) r = r

K= 2.π.r

(2) 2r = r

K = 2.π.2.r

K = π.4.r

Jadi, yang kelilingnya lebih besar adalah setengah lingkaran dengan jari-jari 2r.

8. Pada gambar di samping adalah dua lingkaran yang konsentris di titik pusat E. Jika m∠1 = 42°,

Tentukan syarat apa yang harus dipenuhi agar panjang busur AB sama dengan dua kali panjang busur CD.

Jawaban:

Lingkaran yang kosentris artinya lingkaran yang mempunyai titik pusat yang sama.

Panjang busur=(α/360°)× keliling lingkaran

Atau

Panjang busur=(α/360°)×2πr

PAB = 2PCD

42/360 x 2 πr2 = 2 x 42/360 x 2 πr1

Sederhanakan kedua ruas, maka didapat:

r2 = 2r1

Jadi, syarat yang harus dipenuhi agar panjang busur AB sama dengan dua kali panjang busur CD adalah panjang jari-jari lingkaran 2 sama dengan panjang dua kali jari-jari lingkaran 1.

(lingkaran 2 adalah lingkaran besar, lingkaran 1 adalah lingkaran kecil pada gambar)

9. Bandingkan keliling lingkaran E dengan persegi panjang ABCD pada gambar di samping.

Tentukan pernyataan yang benar.

a. Keliling persegi panjang ABCD lebih dari keliling lingkaran E.

b. Keliling lingkaran E lebih dari persegi panjang ABCD

c. Keliling lingkaran E sama dengan persegi panjang ABCD

d. Tidak cukup informasi untuk menentukan perbandingan kelilingnya.

Jawaban:

Pada gambar tersebut, terdapat dua bidang datar, yaitu persegi panjang ABCD dan lingkaran dengan titik pusat di E.

Pada bangun persegi panjang ABCD ini, panjang sisi AB dan DC adalah sama dengan diameter lingkaran, atau sama dengan 2 kali radius (jari-jari) lingkaran.

Sementara, panjang sisi AD dan BC adalah sama dengan radius (jari-jari) lingkaran.

Jika kita misalkan radius lingkaran yang berpusat di E adalah r maka, panjang sisi AB dan DC adalah 2r dan panjang sisi AD dan BC adalah r.

Sehingga:

1. Keliling persegi panjang ABCD adalah:

keliling ABCD = 2 (panjang + lebar)

= 2 (2r + r)

= 2(3r)

= 6r

2. Keliling lingkaran E adalah:

keliling lingkaran = 2 π r

= 2 (3,14) r

= 6,28 r

Berdasarkan perhitungan tersebut, terlihat bahwa keliling lingkaran E lebih besar dari keliling persegi panjang ABCD (6,28 r > 6 r).

Sehingga pernyataan yang benar adalah b. Keliling lingkaran E lebih dari keliling persegi panjang ABCD.

Demikian kunci jawaban Matematika kelas 8 halaman 93 94, kegiatan siswa ayo kita berlatih 7.3: soal essay nomor 1-9 sesuai dengan kurikulum 2013 edisi revisi tahun 2017.

Disclaimer

Kunci jawaban diatas bersifat alternatif jawaban sehingga para siswa bisa memberikan eksplorasi jawaban lain.

Kunci jawaban soal diatas bisa saja berbeda sesuai dengan pemahaman tenaga pengajar atau murid. (*)