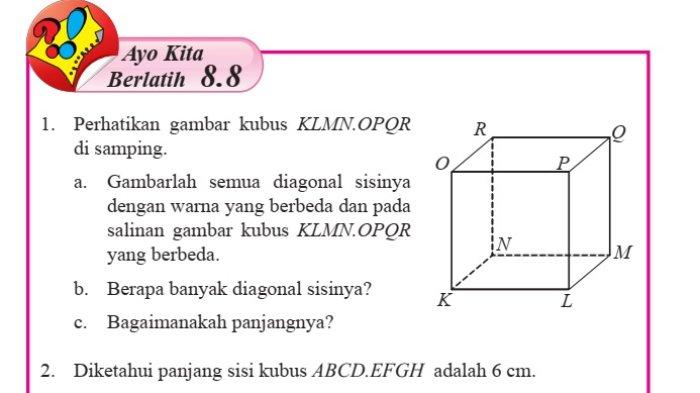
Ayo Kita Berlatih 8.8, Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 213 214 Terlengkap

= √(122 + 92)

= √(144 + 81)

=  √225

= 15 cm

Luas ACE = 1/2 x AE X AC

= 1/2 x 8 x 15

= 60 cm⊃2;

Jadi, luas daerah segitiga ACE adalah 60 cm⊃2;.

4. Perhatikan gambar berikut.

Tentukan luas permukaan prisma ABE.DCH.

Jawaban:

EB = √(EA⊃2; + AB⊃2;)

= √(82 + 152)

= √(64 + 225)

=  √289

= 17cm

Luas permukaan ABE.DCH = (AB x BC) + (EB x BC) + (EA x AD) + (2 x 1/2 x EA x AB)

= (15 x 4) + (17 x 4) + (8 x 4) + (2 x 1/2 x 8 x 15)

= 60 + 68 + 32 + 120

= 280 cm⊃2;

Jadi, luas permukaan prisma ABE.DCH adalah 280 cm⊃2;.

5. Gambar di samping menunjukkan sebuah kubus dengan panjang rusuk 5 cm yang dipotong sehingga salah satu bagiannya berbentuk limas segitiga (tetrahedron).

Tentukan volume kedua bangun hasil perpotongannya.

Jawaban:

Volume limas = 1/3 x luas alas x tinggi

= 1/3 x (1/2 x 5 x 5) x 5

= 125/6 cm⊃3;

Volume kubus = s x s x s

= 5 x 5 x 5

= 125 cm⊃3;

Volume potongan kubus = Volume kubus - Volume limas

= 125 - 125/6

= 750/6 - 125/6

= 625/6 cm⊃3;

Jadi, volume bangun limas adalah 125/6 cm⊃3;, dan volume bangun lainnya adalah 625/6 cm⊃3;.

6. Q merupakan titik perpotongan dua diagonal sisi kubus yang panjang rusuknya 2 cm.

Tentukan panjang QR.

Jawaban:

QP = 1/2 x √(s⊃2; + s⊃2;)

= 1/2 x √(2⊃2; + 2⊃2;)

= 1/2 x √8

= 1/2 x 2√2

= √2 cm

QR = √(RP⊃2; + QP⊃2;)

= √(2⊃2; + √2⊃2;)

= √(4 + 2)

= √6 cm

Jadi, panjang QR adalah √6 cm.

7. ABCD.EFGH adalah kubus dengan rusuk 10 cm.

Titik X, Y, dan Z adalah pertengahan EH, BG dan AB. Hitunglah panjang XZ, YZ, dan XY.

Jawaban:

XY = √(s⊃2; + (1/2 x s)⊃2;)

= √(10⊃2; + (1/2 x 10)⊃2;)

= √(100 + 25)

= √125

= 5√5 cm

YZ = 1/2 x s√3

= 1/2 x 10 √3

= 5√3 cm

XZ = 1/2 x s√6

= 1/2 x 10√6

= 5√6 cm

Jadi, panjang XY adalah 5√5 cm, panjang YZ adalah 5√3 cm, dan panjang XZ adalah 5√6 cm.

8. Perhatikan gambar prisma berikut ini. 

Diketahui alas prisma tersebut berbentuk segitiga siku-siku dengan panjang BC = 3 cm dan AC = 4 cm.

Jika luas permukaan prisma 108 cm⊃2;, tentukan tinggi prisma tersebut. Bagaimana cara kalian mencari luas bidang ABF? Jelaskan.

Jawaban:

AB = √(AC⊃2; + BC⊃2;)

= √(4⊃2; + 3⊃2;)

= √(16 + 9)

= √25

= 5 cm

Luas permukaan = (2 x luas alas) + (keliling alas x tinggi)

108 = (2 x 1/2 x 4 x 3) + ((5 + 4 + 3) x tinggi)

108 = 12 + 12 x tinggi

tinggi = (108 - 12)  / 12

tinggi = 8cm

Jadi, tinggi prisma tersebut adalah 8 cm.

Salah satu cara untuk mencari luas bidang ABF yaitu dengan terlebih dahulu mencari panjang FA dan FB, kemudian mencari luas segitiga ABF dengan formula heron: Luas ∆ABC = √(s(s – a)(s – b)(s – c)).

9. Perhatikan gambar prisma segilima di samping. 

Tentukan:

a. ada berapa banyak rusuknya?

b. ada berapa banyak bidang sisinya?

c. ada berapa banyak titik sudutnya?

d. hubungkan titik sudut A dengan titik sudut D, apakah termasuk diagonal bidang? Coba jelaskan.

e. hubungkan titik sudut A dengan titik sudut H, apakah termasuk diagonal ruang? Coba jelaskan.

f. hubungkan titik-titik A, C, H, dan F, apakah termasuk bidang diagonal? Coba jelaskan.

Jawaban:

a. Banyak rusuk = 15

b. Banyak bidang sisi = 7

c. Banyak titik sudut = 10

d. Tidak, karena titik A dengan titik D adalah diagonal sisi.

e. Ya, karena terletak di dalam bangun ABCDE.FGHIJ

f. Ya, karena memotong bangun menjadi 2 ruang.

Demikian kunci jawaban Matematika kelas 8 halaman 213 214, kegiatan siswa ayo kita berlatih 8.8 lengkap dengan pembahasan sesuai dengan buku Matematika kurikulum 2013 edisi revisi tahun 2017.

Disclaimer

Kunci jawaban diatas bersifat alternatif jawaban sehingga para siswa bisa memberikan eksplorasi jawaban lain.

Kunci jawaban soal diatas bisa saja berbeda sesuai dengan pemahaman tenaga pengajar atau murid. (*)