Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 270 271 272, Soal Ayo Kita Berlatih 8.6: Part 1

TRIBUN-BALI.COM, DENPASAR – Mari kita belajar! Berikut ini kunci jawaban Matematika Kelas 7 Semester 2 halaman 270 271 272, soal kegiatan siswa Ayo Kita Berlatih 8.6: Part 1.

Kali ini kita akan membahas soal pada bab ke 8 yang berjudul Segiempat dan Segitiga pada kegiatan siswa ayo kita berlatih 8.6: Part 1 soal nomor 1 – 10.

Kunci jawaban di bawah ini diharapkan bisa membantu siswa sebagai alternatif jawaban untuk menyelesaikan soal pada halaman 270 271 272 di buku siswa Matematika Kelas 7.

Berikut kunci jawaban dan pembahasan soal Matematika Kelas 7 Semester 2 halaman 270 271 272 sesuai dengan buku Matematika Kurikulum 2013 edisi revisi tahun 2017.

Baca juga: Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 254 255, Soal Ayo Kita Berlatih Aktivitas 8.5

(Update Kunci Jawaban)

Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 270 271 272

Ayo Kita Berlatih 8.6

Part 1 Nomor 1-10

Soal nomor 1

Tentukan keliling segitiga, pada gambar di bawah ini.

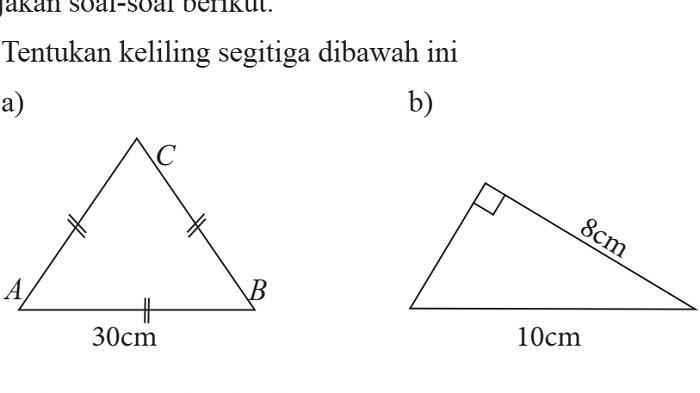
Jawaban:

a. Diketahui: segitiga adalah segitiga sama sisi.

Maka semua sisinya memiliki ukuran yang sama.

K = 3(s)

K = 3 (30)

K = 90 cm

Jadi keliling segitiga ABC adalah 90 cm.

b. Diketahui: segitiga adalah segitiga siku-siku.

Kita perlu mengetahui ukuran sisi alas dengan menggunakan rumus Phytagoras.

a = √(102 - 82)

= √(100 - 64)

= √36

= 6cm

K = a + b + c

= 6 + 8 + 10

= 24 cm

Jadi, keliling segitiga siku-siku itu adalah 24 cm.

Baca juga: Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 244, Soal Ayo Kita Berlatih Aktivitas 8.4 Part 2

Soal nomor 2

Luas ∆ABC pada gambar di bawah ini adalah ...

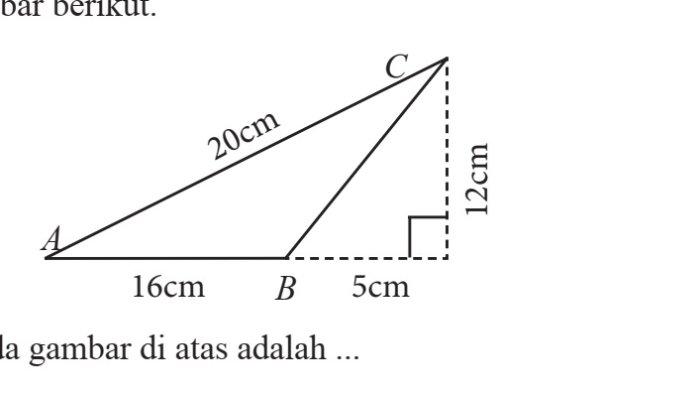
a. 30 cm2

b. 66 cm2

c. 96 cm2

d. 120 cm2

Jawaban:

Luas ABC = luas segitiga siku-siku keseluruhan - luas segitiga siku-siku kecil

= (1/2 x (16 + 5) x 12) - ( 1/2 x 5 x 12)

= 126 - 30

= 96 cm2

Jadi, luas segitiga ABC pada gambar diatas adalah C.96 cm2

Soal nomor 3

Luas sebuah segitiga 84 cm2 dan panjang alasnya 12 cm.

Tinggi segitiga tersebut adalah ...

a. 7 cm

b. 14 cm

c. 24 cm

d. 30 cm

Jawaban:

Luas segitiga = 1/2 x panjang alas x tinggi

84 = 1/2 x 12 x tinggi

tinggi = 84 x 2 / 12

= 14 cm

Jadi, tinggi segitiga adalah A. 7 cm.

Baca juga: Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 242 243, Soal Ayo Kita Berlatih Aktivitas 8.4

Soal nomor 4

Perbandingan alas dan tinggi sebuah segitiga adalah 5 : 4.

Jika luas segitiga tersebut 160 cm2, maka tingginya adalah ...

a. 4 cm

b. 16 cm

c. 20 cm

d. 32 cm

Jawaban:

Luas alas = 1/2 x panjang alas x tinggi

160 = 1/2 x 5a x 4a

10a2 = 160

a2 = 160/10

a = √16

a = 4 cm

Alas = 5a = 5 x 4 = 20 cm

Tinggi = 4a = 4 x 4 = 16 cm

Jadi, tinggi segitiga adalah B. 16 cm.

Soal nomor 5

Sebuah taman berbentuk persegi panjang dengan ukuran panjang 25 m dan lebar 20 m.

Di dalam taman terdapat pot bunga yang berbentuk 2 segitiga siku-siku yang kongruen dengan ukuran panjang sisi siku sikunya 8 m dan 6 m. dan sisanya ditanami rumput.

Hitunglah luas tanaman rumput tersebut?

Jawaban:

Luas rumput = luas taman - (2 x luas pot bunga segitiga )

= (p x l ) - ( 2 x 1/2 x alas x tinggi )

= (25 x 20) - ( 2 x 1/2 x 8 x 6 )

= 500 - 48

= 452 cm2

Jadi, luas tanaman rumput adalah 452 cm2.

Soal nomor 6

Suci mempunyai satu lembar karton bermotif berbentuk persegi dengan panjang sisinya 25 cm.

Suci akan membuat mainan yang berbentuk seperti pada gambar di bawah.

Berapakah luas karton yang tidak terpakai?

Jawaban:

Luas karton tidak terpakai terpakai = luas karton - luas segitiga

= (s x s) - (1/2 x s x s)

= (25 x 25) - (1/2 x 25 x 25)

= 625 - 625/2

= 312,5 cm2

Jadi, luas karton yang tidak terpakai adalah 312,5 cm2.

Soal nomor 7

Hitunglah luas bangun PQRS pada gambar berikut!

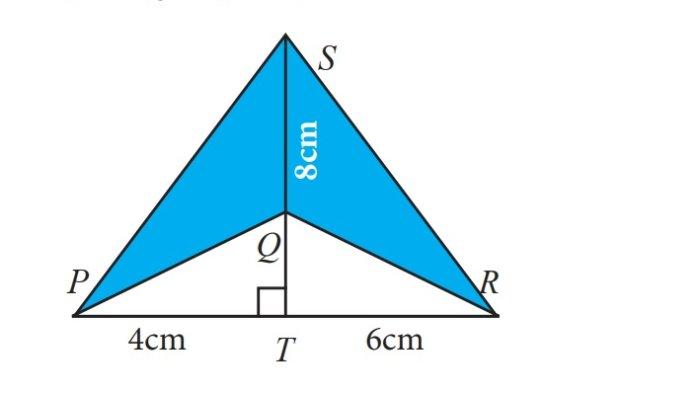
Jawaban:

Luas PQRS = Luas PTRS - Luas PQRT

= (1/2 x PR x ST) - (1/2 x PR x QT)

= (1/2 x (4 + 6) x (h+8)) - (1/2 x (4+6) x h)

= (5h + 40) - 5h

= 40 cm2

Jadi, luas PQRS adalah 40 cm2.

Soal nomor 8

Perhatikan daerah segitiga I dan II. Bandingkan luas I dan luas II. Jelaskan

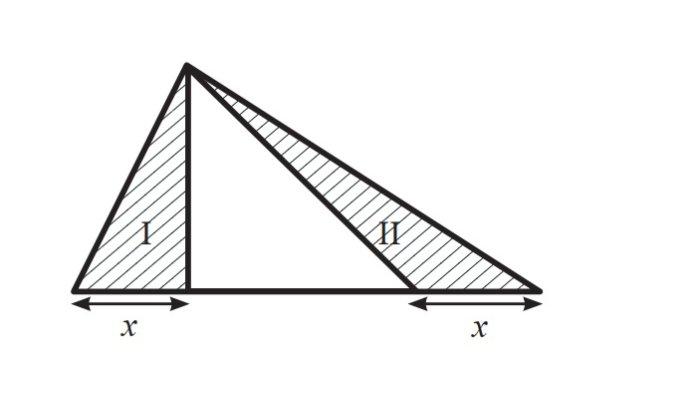
Jawaban:

Bandingkan luas I dan luas II adalah 1 : 1

Karena memiliki panjang alas dan tinggi yang sama.

Soal nomor 9

Jika panjang AB = 16 cm, maka luas bangun ABCDE adalah ....

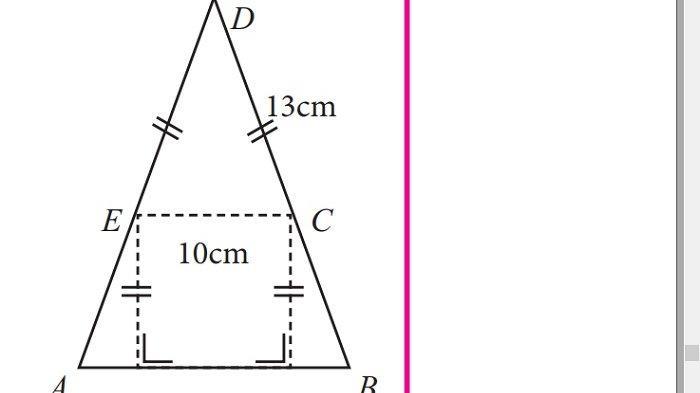
a. 164 cm2

b. 190 cm2

c. 229 cm2

d. 250 cm2

Jawaban:

Tinggi Segitiga di atas kotak = √(DC2 - (1/2 x EC)2)

= √(132 - (1/2 x 10)2)

= √(169 - 25)

= √144

= 12 cm

Luas ABCDE = (2 x luas segitiga kecil) + luas kotak + luas segitiga besar

= (2 x 1/2 x 3 x 13) + (13 x 10) + (1/2 x 10 x 12)

= 39 + 130 + 60

= 229 cm2

Jadi, luas segitiga ABCDE adalah C. 229 cm2.

Soal nomor 10

Pada segitiga ABC yang tumpul di C, titik M adalah titik tengah AB.

Melalui C dibuat garis tegak lurus pada BC yang memotong AB di titik E.

Dari M, ditarik garis memotong BC yang tegak lurus di D.

Jika luas segitiga ABC adalah 54 satuan luas.

Maka luas segitiga BED adalah...

Jawaban:

Luas segitiga BED = 1/2 x luas ABC

= 1/2 x 54

= 27 satuan

Jadi, luas segitiga BED adalah 27.

Demikian kunci jawaban Matematika Kelas 7 Semester 2 halaman 270 271 272, soal kegiatan siswa Ayo Kita Berlatih 8.6: Part 1 sesuai dengan Kurikulum 2013 edisi revisi tahun 2017.

Disclaimer

Kunci jawaban diatas bersifat alternatif jawaban sehingga para siswa bisa memberikan eksplorasi jawaban lain.

Kunci jawaban soal diatas bisa saja berbeda sesuai dengan pemahaman tenaga pengajar atau murid. (*)