Kunci Jawaban Matematika Kelas 8 Semester 1 Halaman 127 128 129 130, Uji Kompetensi Bab 3

A. –3

B. –4

C. –5

D. –6

8. Diketahui fungsi f : x → 2x – 1. Pernyataan di bawah ini yang salah adalah ....

A. 3 → 4

B. f(–5) = –11

C. jika f(a) = 5, maka a = 3

D. bayangan 1 adalah 1

9. Diketahui G(x) = ax + b. Jika G(–2) = –4 dan G(–6) = 12, maka bentuk fungsi G adalah ....

A. G(x) = –4x + 12

B. G(x) = –4x – 12

C. G(x) = –2x + 6

D. G(x) = –4x – 6

10. Daerah asal fungsi yang didefinisikan dengan fungsi f dari x ke 2x – 1 adalah {x | −2x < x>

A. {–3, –1, 1, 3}

B. {–2, –3, –1, 1, 3, 4}

C. {–2, –1, 0, 1, 3}

D. { –1, 0, 1, 2}

11. Jika A = {2, 3, 5, 7} dan B = {4, 6, 8, 9, 10}, banyaknya pemetaan yang mungkin dari A ke B dan dari B ke A berturut-turut adalah ....

A. 225 dan 425

B. 525 dan 225

C. 525 dan 256

D. 625 dan 256

12. Fungsi f ditentukan oleh f(x) = ax + b. Jika nilai dari fungsi itu untuk x = –3 adalah –15 dan nilai dari fungsi itu untuk x = 3 adalah 9, nilai dari f(−2) + f(2) adalah ....

A. –6

B. –4

C. 4

D. 6

13. Fungsi f ditentukan oleh f(x) = ax + b. Jika pasangan-pasangan berurutan (p, −3), (−3, q), (r, 2), (2, −2), dan (−2, 6) adalah anggota dari fungsi itu, nilai p, q, dan r adalah ....

A. p = 5, q = 6, dan r = 2

B. p = 3/2, q = 8, dan r = 2

C. p = 5/2, q = 8, dan r = 0

D. p = 3, q = 6, dan r = 3

14. Diketahui fungsi f(x) = mx + n, f(–1) = 1, dan f(1) = 5. Nilai m dan n berturut-turut adalah…

A. –2 dan –3

B. 2 dan –3

C. –2 dan 3

D. 2 dan 3

15. Jika f(2x + 1) = (x – 12)(x + 13), maka nilai dari f(31) adalah ....

A. 46

B. 64

C. 66

D. 84

16. Misalkan f(x) adalah fungsi yang memenuhi (a) untuk setiap bilangan real x dan y, maka f(x + y) = x + f(y) dan (b) f(0) = 2 Nilai dari f(2.016) adalah ....

A. 2.015

B. 2.016

C. 2.017

D. 2.018

17. Diketahui fungsi bilangan real f(x) = x/1-x, untuk x ≠ 1 Nilai dari f(2.016) + f(2.015) + ... + f(3) + f(2) + f(1/2) + f(1/3)+ ... + adalah ...

A. –4.034

B. –4.032

C. –4.030

D. –4.028

18. Untuk setiap bilangan bulat x didefinisikan fungsi f dengan f(x) adalah banyaknya angka (digit) dari x. Contoh: f(216) = 3, dan f(2.016) = 4. Nilai f(22.016) + f(52.016) adalah ....

A. 2.015

B. 2.016

C. 2.017

D. 2.018

19. Perhatikan diagram berikut ini.

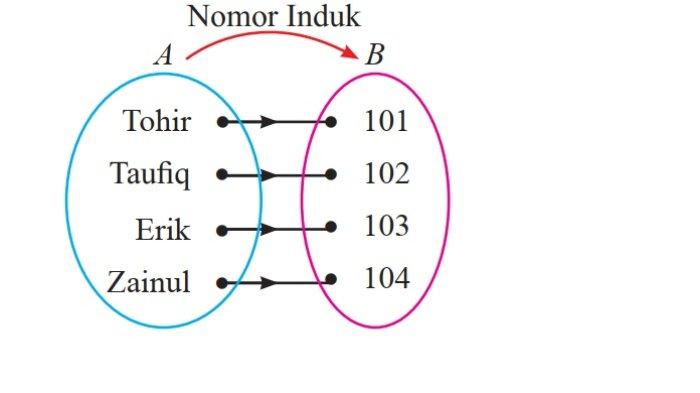
Pernyataan yang dapat kamu simpulkan dari diagram panah di atas adalah sebagai berikut.

(i) Setiap siswa tepat mempunyai nomor induk satu. Jadi, setiap anggota A hanya mempunyai tepat satu dengan anggota B.

(ii) Dengan demikian pengertian dari korespondensi satu-satu adalah beberapa dari anggota himpunan A maupun dari anggota B hanya mempunyai satu kawan.

(iii) Setiap siswa bisa mempunyai nomor induk lebih dari satu. Jadi, setiap anggota A bisa mempunyai lebih satu dengan anggota B.

(iv) Dengan demikian pengertian dari korespondensi satu-satu adalah setiap dari anggota himpunan A maupun dari anggota B hanya mempunyai satu kawan.

Pernyataan yang benar dari kesimpulan di atas adalah ….

A. (i) dan (ii)

B. (ii) dan (iii)

C. (i) dan (iv)

D. (ii) dan (iv)

20. Jika X = {2, 3, 5, 7, 11} dan Y = { a, b, c, d, e}, banyaknya korespondensi satu-satu yang mungkin terjadi adalah ....

A. 24

B. 120

C. 540

D. 720

Jawaban:

1. B

2. C

3. B

4. D

5. B

6. B

7. B

8. A

9. B

10. A

11. D

12. A

13. C

Petunjuk:

Langkah pertama temukan persamaan fungsi dari dua himpunan pasangan berurutan (2, –2); dan (–2, 6) melalui bentuk umum dari f(x) = ax + b

Langkah kedua nilai p, q, dan r berdasarkan persamaan fungsi yang diketahui Jadi, nilai p = 2/Kemudian terapkan bentuk f(–2.016 + 2.016) ke-persamaan fungsi dari f(x + y) = x + f(y), maka akan diperoleh f(2.016) = 2.018

Jadi, nilai dari f(2.016) adalah 2.018.

14. D

15. D

Petunjuk:

Tentukan nilai x yang memenuhi untuk f(31). Substitusikan nilai x tersebut ke persamaan fungsinya f(2x + 1) = (x – 12)(x + 13), baru kemudian akan ketemu nilai f(31) = 84 Jadi, nilai dari f(31) adalah 84.

16. D

Petunjuk:

Gunakan persamaan fungsi dari f(0) menjadi f(–2.016 + 2.016) Kemudian terapkan bentuk f(–2.016 + 2.016) ke-persamaan fungsi dari f(x + y) = x + f(y), maka akan diperoleh f(2.016) = 2.018 Jadi, nilai dari f(2.016) adalah 2.018.

17. C

Petunjuk:

Gunakan persamaan fungsi dari f(x) = x/1/x untuk menentukan nilai dari semua fungsi. Kemudian mencari pola penyelesaian dari bentuk soal diatas, yakni dengan memerhatikan nilai fungsi dari ujung ke ujung dan begitu seterusnya, sehingga ketemu –4.030.

18. C

Petunjuk:

Mencari pola dari penjumlahan f(2^n) + f(5^n), dengan n bilangan asli Jika n = 1, berapakah nilai dari f(2^1) + f(5^1) Jika n = 2, berapakah nilai dari f(2^2) + f(5^2) Dan seterusnya.

Sehingga pada akhirnya akan ketemu pola yang bersesuaian.

19. C

20. B

Demikian kunci jawaban Matematika Kelas 8 Semester 1 halaman 127 128 129 130, soal kegiatan siswa Uji Kompetensi Bab 3: Pilihan Ganda sesuai dengan Kurikulum 2013 edisi revisi tahun 2017.

Disclaimer

Kunci jawaban diatas bersifat alternatif jawaban sehingga para siswa bisa memberikan eksplorasi jawaban lain.

Kunci jawaban soal diatas bisa saja berbeda sesuai dengan pemahaman tenaga pengajar atau murid. (*)