Kunci Jawaban Matematika Kelas 8 Semester 1 Halaman 227, Ayo Kita Menalar: Persamaan Konstanta

TRIBUN-BALI.COM, DENPASAR – Mari kita belajar! Simak nih, inilah kunci jawaban Matematika Kelas 8 Semester 1 halaman 227, Ayo Kita Menalar: Persamaan Konstanta.

Kali ini kita akan membahas soal pada bab ke 5 yang berjudul Sistem Persamaan Linear Dua Variabel pada kegiatan siswa Ayo Kita Menalar tentang eliminasi dengan persamaan konstanta.

Kunci jawaban di bawah ini diharapkan bisa membantu siswa sebagai alternatif jawaban untuk menyelesaikan soal pada halaman 227 di buku siswa Matematika Kelas 8.

Berikut kunci jawaban dan pembahasan soal Matematika Kelas 8 Semester 1 halaman 227 sesuai dengan buku Matematika Kurikulum 2013 edisi revisi tahun 2017.

Baca juga: Kunci Jawaban Matematika Kelas 7 Kurikulum Merdeka Halaman 50 51 52 53, Latihan 2.1: Bilangan

(Update Kunci Jawaban)

Kunci Jawaban Matematika Kelas 8 Semester 1 Halaman 227

Ayo Kita Menalar

Kalian telah mengetahui cara menyelesaikan sistem persamaan linear dua variabel dengan metode eliminasi.

Pada saat kalian mengeliminasi salah satu variabel, langkah pertama yang kalian lakukan adalah mengalikan persamaan dengan konstanta.

a. Perhatikan strategi yang digunakan Lisa untuk menentukan harga tiap-tiap jenis lilin.

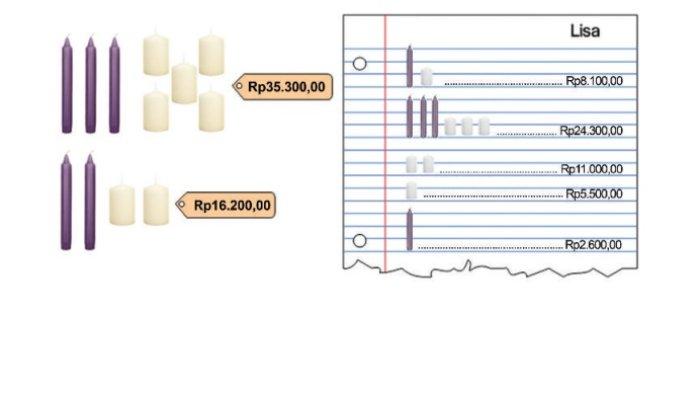
Jelaskan strategi yang digunakan Lisa untuk menentukan harga sebuah lilin ungu dan sebuah lilin putih.

Baca juga: Kunci Jawaban Matematika Kelas 7 Kurikulum Merdeka Halaman 49 50, Ayo Mencoba: Garis Bilangan

b. Kapan kalian harus mengalikan persamaan dengan konstanta untuk menyelesaikan sistem persamaan linear dengan menggunakan eliminasi? Jelaskan.

c. Mengapa dengan mengalikan persamaan dengan konstanta tidak mengubah selesaian dari sistem persamaan? Jelaskan alasan kalian.

d. Selesaian dari suatu sistem persamaan linear dua variabel adalah (2, −4).

Salah satu persamaan dalam sistem persamaan adalah 2x + y = 0. Jelaskan bagaimana cara kalian untuk menentukan persamaan kedua untuk sistem persamaan linear tersebut.

Kemudian, tentukan persamaan kedua. Selanjutnya, selesaikan sistem persamaan yang telah kalian temukan dengan metode eliminasi untuk menguji kebenaran jawaban kalian.

e. Kalian menyelesaikan sistem persamaan linear dua variabel dengan x menyatakan banyaknya tiket dewasa yang terjual dan y menyatakan banyaknya tiket anak-anak yang terjual.

Baca juga: Kunci Jawaban Matematika Kelas 7 Kurikulum Merdeka Halaman 48 49, Eksplorasi 2.3: Bilangan Rasional

Dapatkah (−6, 24) menjadi selesaian dari sistem persamaan linear dua variabel? Jelaskan alasan kalian.

a. Strategi yang digunakan Lisa adalah dengan menggunakan eliminasi. Lisa memisalkan harga sebuah lilin ungu adalah x dan harga sebuah lilin putih adalah y.

Sistem persamaan linear dua variabel yang terbentuk adalah 3x + 2y = 35.300 dan 2x + 2y = 16.200.

Selanjutnya, Lisa membagi persamaan kedua dengan 2 sehingga diperoleh persamaan x + y = 8.100.

Setelah itu, persamaan tersebut dikalikan 3 sehingga diperoleh 3x + 3y = 24.300. Kemudian, Lisa mengeliminasi variabel x sehingga diperoleh 2x = 11.000 dan x = 5.500.

Terakhir, Lisa bisa menentukan nilai y = 2.600.

b. Mengalikan persamaan dengan suatu konstanta apabila setiap variabel pada kedua persamaan memiliki koefisien yang berbeda.

c. Karena mengalikan persamaan dalam metode eliminasi ini hanya menyamakan koefisien pada salah satu variabel kedua persamaan sehingga keduanya dapat dieliminasi.

Oleh karena itu, mengalikan persamaan dengan suatu konstanta tidak mengubah selesaian.

d. Persamaan kedua supaya selesaian dari sistem persamaan linear dua variabel adalah (2, −4) adalah x + y = −2.

Cara untuk menentukan persamaan kedua adalah dengan membuat sebarang persamaan sedemikian sehingga, apabila nilai x dan y pada persamaan diganti oleh (2, −4) menjadikan persamaan menjadi benar.

Perhatikan bahwa

x + y = −2

2 + (−4) = −2

−2 = −2

Untuk menguji kebenaran apakah (2, −4) adalah selesaian dari Sistem persamaan linear dua variabel 2x + y = 0 dan x + y = −2, maka metode eliminasi dapat diterapkan seperti berikut.

2x + y = 0

x + y = −2 –

____________

x = 2

Dengan mensubstitusikan nilai x = 2 ke persamaan pertama, diperoleh

2x + y = 0

2(2) + y = 0

4 + y = 0

y = −4

Jadi, benar bahwa (2, −4) adalah selesaian dari Sistem persamaan linear dua variabel 2x + y = 0 dan x + y = −2.

Jawaban siswa pada poin ini akan beragam. Khususnya pada menentukan persamaan linear yang kedua.

e. Selesaian (−6, 24) tidak mungkin menjadi selesaian dari Sistem persamaan linear dua variabel yang dimaksud pada situasi di atas.

Nilai x = −6 tidak mungkin menyatakan banyak tiket dewasa yang terjual. Hal ini dikarenakan bahwa banyak tiket tidak bisa dinyatakan dengan bilangan negatif.

Demikian kunci jawaban Matematika Kelas 8 Semester 1 halaman 227, soal kegiatan siswa Ayo Kita Menalar: Persamaan Konstanta sesuai dengan Kurikulum 2013 edisi revisi tahun 2017.

Disclaimer

Kunci jawaban diatas bersifat alternatif jawaban sehingga para siswa bisa memberikan eksplorasi jawaban lain.

Kunci jawaban soal diatas bisa saja berbeda sesuai dengan pemahaman tenaga pengajar atau murid. (*)