Jawaban Latihan 4.2, Kunci Jawaban Matematika Kelas 7 Halaman 143 144 145 Kurikulum Merdeka

TRIBUN-BALI.COM, DENPASAR – Berikut ini jawaban soal kegiatan siswa Latihan 4.2, kunci jawaban Matematika kelas 7 halaman 143 144 145 Kurikulum Merdeka.

Kali ini kita akan membahas soal pada bab ke 4 yang berjudul Bentuk Aljabar sesuai dengan buku Matematika kelas 7 Kurikulum Merdeka edisi tahun 2022.

Jawaban Matematika Kelas 7 Halaman 143 144 145 Kurikulum Merdeka

Soal yang akan kita selesaikan adalah soal pada halaman 143 144 145 pada kegiatan siswa Latihan 4.2: menuliskan setiap aljabar dalam bentuk jabaran.

Jawaban di bawah ini diharapkan bisa membantu siswa sebagai alternatif jawaban untuk menyelesaikan soal pada halaman 143 144 145 di buku siswa Matematika kelas 7.

Baca juga: Jawaban Eksplorasi 4.3, Kunci Jawaban Matematika Kelas 7 Halaman 140 Kurikulum Merdeka

Latihan 4.2

1. Tulislah setiap bentuk aljabar berikut dalam bentuk jabaran.

a. 3(x + 2)

b. 8(2x − 5)

c. 2x(x + 5)

d. (x + 1)(x + 3)

Jawaban:

a. 3x + 6

b. 16x – 40

c. 2x^2 – 10x

d. x^2 + 3x + x + 3 = x^2 + 4x+ 3

2. Tulislah setiap bentuk aljabar berikut dalam bentuk faktor.

a. 12x + 6

b. x2 + 2x

c. x + x + x + 3

d. x2 + 5x + 6

Baca juga: Jawaban Latihan 4.1, Kunci Jawaban Matematika Kelas 7 Halaman 132 133 134 135 Kurikulum Merdeka

Jawaban:

a. 6 (2x + 1)

b. x (x + 2)

c. 3x + 3 = 3 (x + 1)

d. (x + 2) (x + 3)

3. Seorang siswa menuliskan jawabannya untuk membuktikan bahwa 2(y + 3) + y mempunyai bentuk yang ekuivalen dengan 3y + 6.

2(y + 3) + y = 2y + 6 + y (1)

= 2y + y + 6 (2)

= (2 + 1)y + 6 (3)

= 3y + 6

Sifat-sifat apa yang digunakan pada tahapan (1), (2), dan (3)?

Baca juga: Jawaban Eksplorasi 4.2, Kunci Jawaban Matematika Kelas 7 Halaman 136 137 138 Kurikulum Merdeka

Jawaban:

(1) sifat distributif

(2) sifat komutatif

(3) sifat distributif

4. Lengkapilah tabel nilai bentuk-bentuk aljabar di bawah ini dengan nilai variabel x yang diberikan pada tabel. Berdasarkan hasil pada tabel di atas

a. Apakah bentuk aljabar (2x + 3) + (4x − 7) ekuivalen dengan bentuk aljabar 6x − 4?

b. Jika menurut kalian kedua bentuk aljabar tersebut ekuivalen, maka buktikan dengan menggunakan sifat-sifat dan operasi aljabar.

Jawaban:

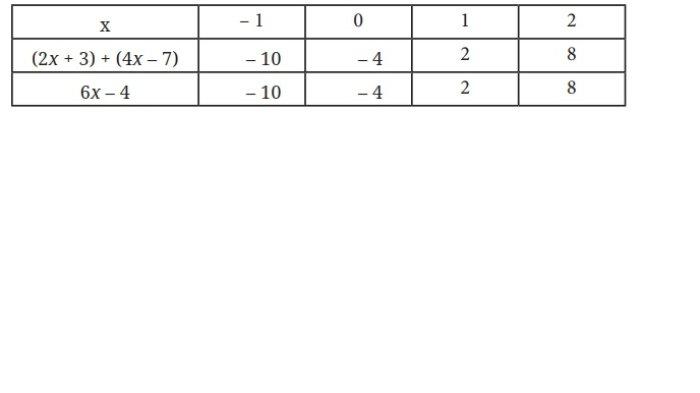
a. Iya, (2x + 3) + (4x – 7) ekuivalen dengan 6x – 4

b. (2x + 3) + (4x – 7) = 2x + 3 + 4x – 7

= 2x + 4x + 3 – 7

= 6x – 4

5. Hitunglah penjumlahan dan pengurangan suku sejenis dengan koefisien berbentuk pecahan berikut ini dengan menggunakan sifat distributif.

a. 1/2x + 1/2x

b. 2/3a + 1/4a

c. 3/2t - 1/2a

d. 1/3m - 1/2m

e. 1/2b^2 - 1/5b^2

Jawaban:

a. 1/2x + 1/2x = (1/2 - 1/2) X = X

b. 2/3a + 1/4a = (2/3 + 1/4) a = 11/12 a

c. 3/2t - 1/2a = (3/2 - 1/2) t = t

d. 1/3m - 1/2m = (1/3 - 1/2) m = - 1/6 m

e. 1/2b^2 - 1/5b^2 = (1/2 + 1/5) b^2 = 7/10 b^2

6. Ayo Berpikir Kritis

Tiga dari bentuk-bentuk aljabar berikut mempunyai bentuk yang ekuivalen. Tentukan bentuk aljabar mana yang tidak ekuivalen dengan ketiga bentuk aljabar tersebut dan jelaskan mengapa.

a. 5x − 2x + 3

b. 3(x + 1)

c. 2x − 5x + 3

d. 3x + 3

Jawaban:

Bentuk a), b) dan d) ekuivalen dengan bentuk 3x + 3 sedangkan bentuk c) dengan bentuk aljabar –3x + 3 tidak ekuivalen dengan a), b) dan d).

7. Ayo Berpikir Kreatif

Tulislah 3 bentuk aljabar yang ekuivalen dengan masing-masing bentuk aljabar berikut ini.

a. 2x + 4

b. 5k – 2

Jawaban:

a. Contoh jawaban: x + x + 2 + 2, 2 (x + 2), 2 (x + 1) + 2

b. Contoh jawaban: 2 (2k – 1) + k, 2 ( 5 k – 1), (3k + 4) + (2k – 6)

8. Ayo Berpikir Kreatif

Berikan sepasang tanda kurung sehingga bentuk aljabar di ruas kiri ekuivalen dengan bentuk aljabar di ruas kanan.

a. 5n + 3 − 3n = 2n + 15

b. 5n + 3 − 3n = 5n

c. 5n + 3 − 3n = 5n2

Jawaban:

a. 5 (n + 3) – 3n = 2n + 15

b. 5n + (3 – 3)n = 5n

c. 5 (n + 3 – 3)n = 5n2

9. Jabarkan, dan jumlahkan atau kurangkan suku-suku sejenis pada bentuk-bentuk aljabar berikut ini.

a. (2x + 2) + (x + 5)

b. (7x − 2) + (−3x + 5)

c. (5x − 1) − (2x + 3)

d. (−3x − 2) − (−2x − 1)

e. 3(x + 10) + 4(3x − 2)

f. 7(2x + 6) − 3(3x + 8)

g. 1/2 (5x - 1) + 3/2 (x - 11)

h. 1/3 (4x + 7) - 1/6 (5x - 11)

Jawaban:

a. 3x + 7

b. 4x + 3

c. 3x – 4

d. –x –1

e. 15x + 22

f. 5x + 18

g. x - 5/2

h. 1/2 x + 25/6

10. Literasi Finansial

Retno melakukan investasi melalui deposito dengan bunga 4 persen per tahun. Retno berencana untuk tidak menarik uangnya sepanjang tahun.

Retno menuliskan sebuah bentuk aljabar P + 0, 04P untuk menyatakan banyak uang pada akhir tahun pertama.

a. Jelaskan mengapa bentuk aljabar tersebut benar.

b. Tulislah bentuk aljabar yang ekuivalen dalam bentuk faktor.

c. Jika Retno melakukan investasi sebesar Rp10.000.000,00,

berapa banyak uang yang dimiliki Retno pada akhir tahun pertama?

Jawaban:

a. P menyatakan uang investasi Retno dan 0,04P menyatakan besar tambahan uang dari bunga yang diperoleh dari investasi sehingga banyak uang Retno adalah P + 0,04P.

b. (1 + 0,04) P

c. (1 + 0,04) P = 1,04 × 10000000 = 10400000

Banyak uang Retno pada akhir tahun adalah Rp10.400.000,00

Keterangan: (^) berarti pangkat

Demikian jawaban soal Matematika kelas 7 Semester 1 halaman 143 144 145 Kurikulum Merdeka, Latihan 4.2 sesuai dengan buku siswa Matematika edisi tahun 2022.

Disclaimer

Kunci jawaban diatas bersifat alternatif jawaban sehingga para siswa bisa memberikan eksplorasi jawaban lain.

Kunci jawaban soal diatas bisa saja berbeda sesuai dengan pemahaman tenaga pengajar atau murid. (*)