Jawaban Soal Latihan 4.2, Kunci Jawaban Matematika Kelas 8 Halaman 172 173 174 Kurikulum Merdeka

TRIBUN-BALI.COM, DENPASAR – Berikut ini jawaban soal kegiatan siswa Soal Latihan 4.2, kunci jawaban Matematika kelas 8 halaman 172 173 174 Kurikulum Merdeka.

Kali ini kita akan membahas soal pada Bab 4 yang berjudul Relasi dan Fungsi sesuai dengan buku Matematika kelas 8 Kurikulum Merdeka edisi tahun 2022.

Jawaban Matematika Kelas 8 Halaman 172 173 174 Kurikulum Merdeka

Soal yang akan kita selesaikan adalah soal pada halaman 172 173 174 pada kegiatan siswa Soal Latihan 4.2: menentukan aturan kata sandi.

Jawaban di bawah ini diharapkan bisa membantu siswa sebagai alternatif jawaban untuk menyelesaikan soal pada halaman 172 173 174 di buku siswa Matematika kelas 8.

Baca juga: Jawaban Ayo Mencoba, Kunci Jawaban Matematika Kelas 8 Halaman 163 164 165 Kurikulum Merdeka

Soal Latihan 4.2

1. Perhatikan dengan cermat terhadap aturan kata sandi berikut ini

Cobalah tulis makna pesan dari kata sandi berikut ini:

a. uxkxax qrqsqi gkqfu zxqax ro ltagsqi

b. gkqfu zxqax qrqsqi uxkxax atzoaq ro kxdqi

Kemudian, cobalah juga sandikan pesan berikut ini:

a. MATEMATIKA ADALAH KEHIDUPANKU

b. SAYA ANAK INDONESIA

Baca juga: Jawaban Ayo Berpikir Kreatif, Kunci Jawaban Matematika Kelas 8 Halaman 160 161 Kurikulum Merdeka

Jawaban:

a. GURUKU ADALAH ORANG TUAKU KETIKA DI SEKOLAH

b. ORANG TUAKU ADALAH GURUKU KETIKA DI RUMAH

c. dqztdqzoaq qrqsqi qtiorxhqfax

d. lqnq qfqa ofrgftloq

2. Himpunan A = {1, 2, 3, 4, 6} dan himpunan B = {2, 4, 6, 8, 10, 12}.

a. Apabila relasi nya adalah "setengah dari", maka tentukan anggota himpunan A yang mempunyai pasangan pada himpunan B. Apakah relasi tersebut merupakan fungsi?

b. Apabila relasinya adalah "kuadrat dari", maka tentukan anggota himpunan B yang mempunyai pasangan pada himpunan A. Apakah relasi tersebut merupakan fungsi?

Jawaban:

a. Himpunan Pasangan Berurutan = {(1, 2), (2, 4), (3, 6), (4, 8), (6, 12)}

Anggota himpunan A yang mempunyai pasangan pada himpunan B adalah {1, 2, 3, 4, 6}. Relasi himpunan A ke B merupakan fungsi.

b. Himpunan Pasangan Berurutan = {(4, 2)} Anggota himpunan B yang mempunyai pasangan pada himpunan A adalah {4}.

Relasi himpunan B ke A merupakan bukan fungsi.

3. Ayo Berpikir Kritis

Farida mengatakan bahwa relasi itu dapat disebut sebagai himpunan bagian dari fungsi, sehingga kedudukan fungsi lebih tinggi dari pada relasi.

Sedangkan Galih mengatakan bahwa saya tidak setuju dengan pendapat Farida. Setujukah kalian dengan pendapat Galih? Jelaskan.

Baca juga: Jawaban Soal Latihan 4.1, Kunci Jawaban Matematika Kelas 8 Halaman 158 159 Kurikulum Merdeka

Jawaban:

Tidak setuju dengan pendapat Galih, karena suatu relasi belum tentu dapat dikatakan sebagai fungsi dan setiap fungsi sudah pasti dapat dikatakan sebagai relasi.

Jadi, kedudukannya lebih tinggi relasi dari pada fungsi, dengan kata lain bahwa fungsi merupakan himpunan bagian dari pada relasi atau lebih luas relasi dari pada fungsi.

4. Ayo Berkomunikasi

Coba perhatikan dan pahami contoh soal dan alternatif penyelesaiannya berikut.

Kemudian coba kalian pikirkan informasi apa yang perlu ditambahkan agar alternatif penyelesaian soal lebih komunikatif lagi.

Jawaban:

Menambahkan anggota himpunan B yang mempunyai pasangan pada himpunan A

Misal:

a. Himpunan pasangan berurutan = {(p, k); (q, k)} anggota himpunan B yang mempunyai pasangan pada himpunan A = {p, q} → termasuk fungsi

b. Himpunan pasangan berurutan = {(p, 1); (p, m)} anggota himpunan B yang mempunyai pasangan pada himpunan A= {p} → termasuk bukan fungsi

5. Periksa apakah dua himpunan berikut ini termasuk fungsi atau bukan fungsi? Jelaskan.

a. Diketahui bahwa himpunan P dan Q memiliki anggota masing masing adalah P = {1, 2, 3, 4, 5} dan Q = {2, 3, 5, 7}.

Apabila "Faktor dari" adalah relasi yang ditentukan, maka dapatkah hubungan antara himpunan P dan Q disebut sebagai fungsi atau bukan fungsi?

b. Diketahui bahwa himpunan R dan S memiliki anggota masing masing adalah R = {3, 4, 6, 8, 9, 12, 14, 18} dan S = {1, 6, 9}.

Apabila “Anggota R sepertiga kali anggota S” adalah relasi yang ditentukan, maka dapatkah hubungan antara himpunan R dan S disebut sebagai fungsi atau bukan fungsi?

Jawaban:

a.

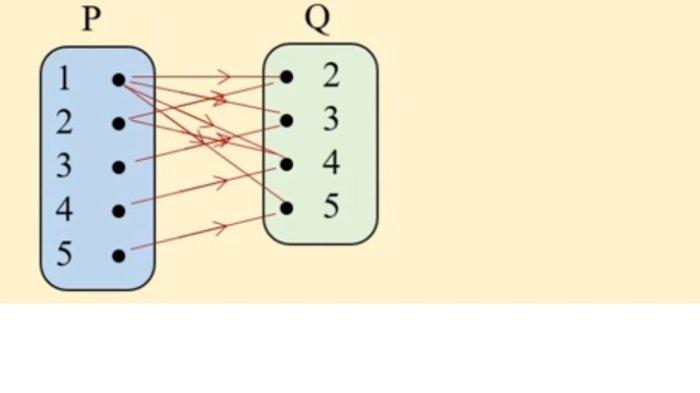
Bukan fungsi karena anggota himpunan P = (1 dan 2) mempunyai pasangan lebih dari satu

b.

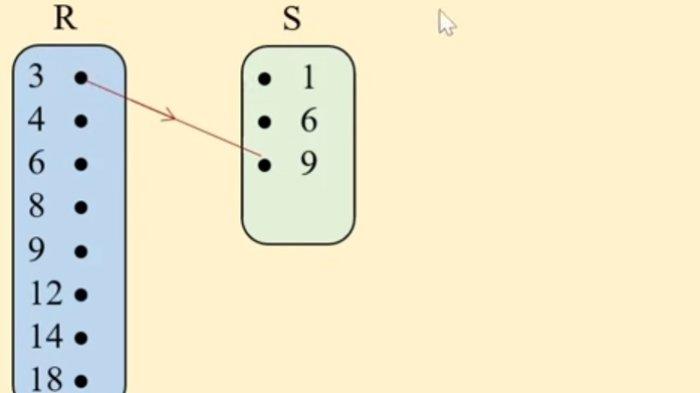
Bukan fungsi karena 4, 6, 8, 9, 12, 14, dan 18 tidak mempunyai pasangan

6. Ayo Berpikir Kreatif

Apabila diketahui himpunan C = {3, 4, 5, 6}; himpunan D = {4, 5, 6, 7}; dan g merupakan fungsi dari himpunan C ke D.

Maka untuk fungsi g, identifikasi tiga aturan yang mungkin dapat digunakan dan nyatakan dengan cara himpunan pasangan berurutan.

Jawaban:

Tiga aturan fungsi yang mungkin di buat:

a. {(3,4), (4, 4), (5, 4), (6,4)}

b. {(3,5), (4, 5), (5, 5), (6, 5)}

c. {(3,6), (4, 6), (5, 6), (6,6)}

7. Diketahui himpunan P merupakan himpunan kuadrat sempurna dari 1 sampai 100, sedangkan himpunan Q adalah himpunan kelipatan 1 sampai 100.

Akar dari adalah relasi yang menghubungkan dari himpunan P ke himpunan Q.

a. Sebutkan semua anggota himpunan P dan himpunan Q.

b. Berdasarkan relasi tersebut, daftar semua pasangan berurutan yang mungkin didapat.

c. Apakah relasi tersebut di atas merupakan fungsi atau bukan fungsi?

d. Apabila relasi tersebut merupakan fungsi, maka sertakan domain, kodomain, dan daerah hasilnya.

Jawaban:

a. P = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}

Q = {1, 2, 3, 4, 5, 6, 7, 8, 9,...100}

b. Jika relasi menghubungkan P ke Q adalah " akar dari" himpunan pasangan berurutan: {(1,1),(4,16), (9,81)}

c.Relasi tersebut adalah merupakan bukan fungsi

d. Domain = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}

Kodomain: {1, 2, 3, 4, 5, 6, 7, 8, 9,...100}

8. Diketahui himpunan E = {p, q} dan himpunan F = { 2, 3, 4 }

a. Nyatakan dengan cara himpunan pasangan berurutan yang membentuk fungsi dari himpunan E ke himpunan F.

b. Temukan ada berapa banyak yang dapat dikatakan fungsi dari himpunan E ke himpunan F.

Jawaban:

a. Himpunan pasangan berurutan yang dimaksud

{(p,2), (q,2)}

{(p,2), (q,3)}

{(p,2), (q,4)}

{(p,3), (q,3)}

{(p,3), (q,2)}

{(p,3), (q,3)}

{(p,3), (q,2)}

{(p,3), (q,4)}

{(p,4), (q,2)}

{(p,4), (q,3)}

{(p,4), (q,4)}

b. banyaknya fungsi yang mungkin dari himpunan A ke himpunan B: ada sebanyak 3^2 = 9

9. Diberikan dua item berikut, tentukan banyaknya fungsi dari himpunan G ke himpunan H:

a. G = {warna lampu lalu lintas} dan H = {warna pelangi}

b. G = {x| x < 7>

H = { - 2 ≤ x < 6>

c. G = {huruf pembentuk kata “INDONESIA”} dan H = {huruf vokal}

Jawaban:

a. G = {merah, kuning, hijau} ~ n(G) = 3

H = {merah, jingga, kuning, hijau, biru, nila, ungu} ~ n(H) =7

Banyak nya fungsi dari himpunan G ke H adalah: 7^3 = 7x7x7 = 343.

b. G={1, 2, 3, 4, 5, 6} n(G)= 6

H = {-2, -1, 0, 1, 2, 3, 4, 5} n(H) = 8

Banyak nya fungsi dari himpunan G ke H adalah:

8^6 = 8×8×8×8×8×8 = 262.144

c. G = {i, n, d, o, e, s, a}~n(G)= 7

H = {a, i, u, e, o } ~n(H)= 5

Banyak nya fungsi dari himpunan G ke H adalah:

5^7 = 5×5×5×5x5x5x5= 78.125

10. Ayo Berpikir Kritis

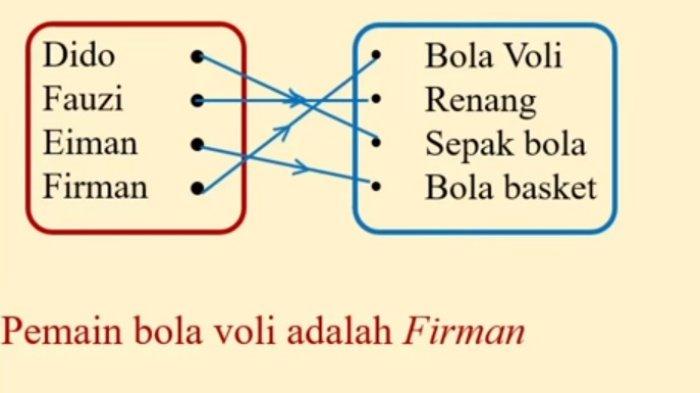
Bola voli, renang, sepak bola, dan bola basket adalah satu satunya cabang olahraga yang ditawarkan di SMP Merdeka Belajar.

Dido, Fauzi, Eiman, dan Firman semuanya merupakan pemain olahraga yang berbeda-beda. Olahraga yang dimainkan Fauzi tidak menggunakan bola.

Eiman seumuran lebih tua dengan pemain bola voli. Eiman dan Firman tidak bermain sepak bola. Bisakah kalian membantu dalam mencari tahu siapa pemain bola voli itu? Jelaskan alasanmu.

Jawaban:

Keterangan: (^) Berarti Pangkat, (/) berarti per atau se-per, (√) berarti akar atau akar dari

Demikian jawaban soal Matematika kelas 8 Semester 2 halaman 172 173 174 Kurikulum Merdeka, Soal Latihan 4.2 sesuai dengan buku siswa Matematika edisi tahun 2022.

Disclaimer

Kunci jawaban diatas bersifat alternatif jawaban sehingga para siswa bisa memberikan eksplorasi jawaban lain.

Kunci jawaban soal diatas bisa saja berbeda sesuai dengan pemahaman tenaga pengajar atau murid. (*)