Kunci Jawaban Matematika Kelas 9 SMP Kurikulum Merdeka Halaman 204 205 206 207 208, Uji Kompetensi

TRIBUN-BALI.COM, DENPASAR – Inilah kunci jawaban Matematika Kelas 9 SMP Kurikulum Merdeka halaman 204 205 206 207 208, pada kegiatan siswa Uji Kompetensi.

Kali ini kita akan membahas soal pada bab 3 yang berjudul Transformasi Geometri pada kegiatan siswa Uji Kompetensi tentang geometri.

Berikut kunci jawaban dan pembahasan soal Matematika Kelas 9 SMP Kurikulum Merdeka halaman 204 205 206 207 208 sesuai dengan buku siswa Matematika edisi tahun 2022.

Baca juga: Kunci Jawaban Matematika Kelas 6 SD Kurikulum Merdeka Halaman 81 82, Eksplorasi 3.1: Bereksplorasi

Uji Kompetensi Bab 3

Jawablah pertanyaan berikut dengan tepat dan jelas!

Uji Pemahaman

Benar atau Salah. Untuk soal nomor 1–10, tentukan apakah pernyataan-pernyataan berikut benar atau salah.

1. Jenis transformasi yang tidak mengalami perubahan ukuran pada bangun datar adalah translasi dan dilatasi.

2. Transformasi yang bayangannya memiliki orientasi berlawanan dengan bentuk awal adalah refleksi.

3. Suatu titik yang ditranslasikan oleh (5|4) dilanjutkan translasi oleh (8|6)akan menghasilkan koordinat yang sama dengan koordinat awal jika ditranslasikan oleh (-3|-2).

4. Suatu titik dirotasikan sebesar 140º yang diikuti dengan rotasi sebesar 260º dengan arah yang sama akan menghasilkan bayangan yang sama jika titik tersebut dirotasikan sebesar 40º.

Baca juga: Kunci Jawaban Matematika Kelas 6 SD Kurikulum Merdeka Halaman 79, Ayo Mengingat Kembali

5. Titik A(3,4) direfleksikan terhadap titik pusat (0,0) akan menghasilkan bayangan yang sama dengan translasi oleh (-6|-8).

6. Dua bangun yang memiliki sudut yang bersesuaian sama besar akan kongruen jika terdapat satu sisi yang bersesuaian sama besar.

7. Bangun A dikatakan kongruen dengan bangun B jika dapat ditunjukkan bahwa bangun A merupakan hasil transformasi dari bangun B.

8. Jika suatu persegi didilatasikan dengan faktor skala 2 maka luas bayangan menjadi 2 kali dari luas persegi awal.

9. Segitiga ABC dengan A(-2,3), B(4,1), C(-2,1) yang didilatasikan terhadap [O,1/2] akan menghasilkan bayangan A'B'C' dengan A'(-1, 3/2), B (2, l/2), C(-1, 1/2).

10 Gambar B merupakan hasil dilatasi dari gambar A dengan faktor skala 2 dan pusat dilatasi O(0,0)

Menggambar. Untuk soal nomor 11–13, salinlah gambar pada kertas berpetak dan lakukan transformasinya.

11. Refleksikan bangun datar berikut terhadap garis refleksi l.

12. Rotasikan bangun datar berikut sebesar 180º terhadap pusat rotasi O.

13. Translasikan bangun datar berikut berdasarkan arah translasi yang diberikan

Untuk nomor 14–15, salinlah bangun datar berikut dan gambarkan bayangan sesuai dengan aturan yang diberikan. Selanjutnya identifikasi jenis transformasinya.

14. (x, y)"(x+3, y)

15. (x, y)"(-x, y)

Isian Singkat. Untuk no 18–22, isilah titik-titik pada pernyataan berikut sehingga menjadi pernyataan lengkap dan benar.

Baca juga: Kunci Jawaban Matematika Kelas 6 SD Kurikulum Merdeka Halaman 74, Pengayaan: Makanan Khas

16. Pencerminan terhadap titik pusat (0,0) akan menghasilkan bayangan yang sama dengan jika dirotasikan sebesar … terhadap titik pusat (0,0).

17. Titik A(3,-4) yang direfleksikan terhadap sumbu x memiliki bayangan di ….

18. Hasil bayangan titik (x,y) yang dirotasikan sebesar 90º berlawanan arah jarum jam terhadap titik pusat (0,0) adalah ….

19. Titik P(-3,2) dicerminkan terhadap sumbu y akan menghasilkan bayangan di titik ….

20. Garis 3x+y=3 ditranslasikan sebesar (-4|3). Bayangannya adalah ….

21. Titik M'(-5,-4) merupakan hasil rotasi sebesar 180º terhadap titik pusat (0,0). Titik awalnya adalah ….

22. Diketahui titik W(u,v) dicerminkan terhadap garis y=3 menghasilkan bayangan di titik W'(-3,2), maka nilai u+v adalah ….

Penerapan

Permainan Golf. Untuk soal 23-24. Dimulai dari titik V, tentukan titik sasaran pada dinding agar bola golf tepat memantul hanya satu kali dari dinding dan masuk ke lubang W.

23. 

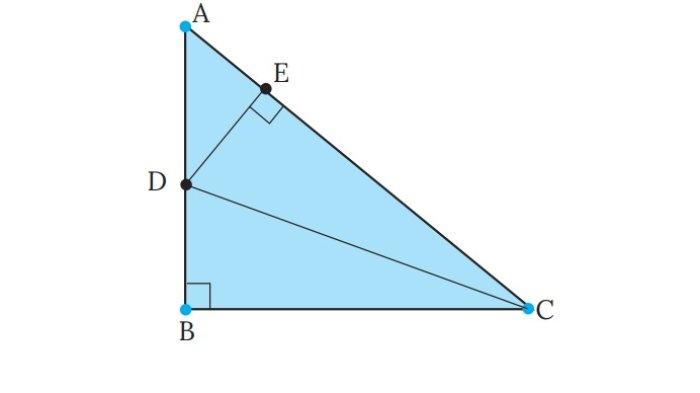
24. 

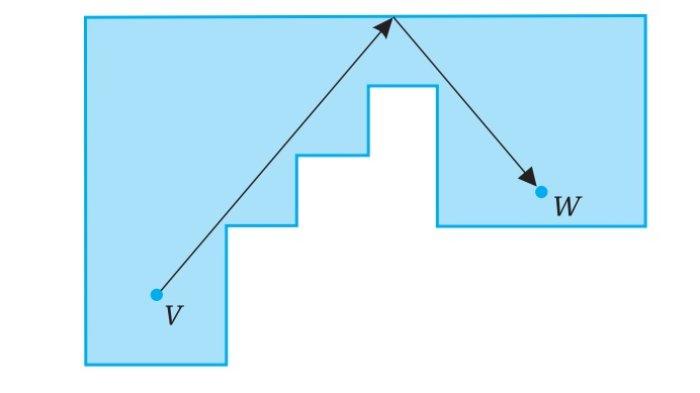
Penalaran

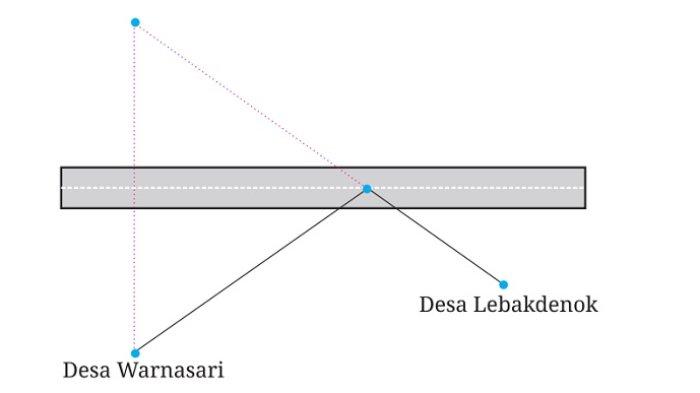
25. Jalan raya sedang dibangun dekat dengan dua desa yaitu Desa Warnasari dan Desa Lebakdenok. Dari kedua desa akan dibangun jalan menuju satu titik persimpangan jalan raya.

Tentukan letak titik persimpangan sehingga jarak dari Desa Warnasari ke Desa Lebakdenok terpendek. Berikan alasanmu!

26. Perhatikan gambar 3.93.

∆ABC siku-siku di B. CD adalah garis bagi ∠BCA dan panjang AB=BC. Tunjukkan bahwa AC=BC+DE!

Jawaban:

Soal nomor 1

Salah. Transformasi dilatasi mengalami perubahan ukuran pada bangun datar dengan faktor skala ≠1.

Soal nomor 2

Ya. Bayangan hasil refleksi memiliki orientasi berlawanan dengan bentuk awal.

Soal nomor 3

Ya. ((x+5)-8, (y+4)-6)=(x-3,y-2).

Soal nomor 4

Ya. 140°+260°=400° bernilai sama dengan 40°.

Soal nomor 5

Salah. A'(-3,-4).

Soal nomor 6

Salah. Syarat kongruen tidak cukup.

Soal nomor 7

Salah. Bangun A dikatakan kongruen dengan bangun B jika bangun A merupakan hasil transformasi kaku atau rigid (translasi, refleksi, dan/atau rotasi) dari bangun B.

Soal nomor 8

Salah. Jika suatu persegi didilatasikan dengan faktor skala 2 maka luas permukaan bayangan menjadi 4 kali dari luas persegi awal.

Soal nomor 9

Benar.

A'{1/2 x (-2), 1/2 x 3} = A'(-1, 3/2)

B' (1/2 x 4, 1/2 x 1) = B' (2, 1/2)

C' {1/2 x (-2), 1/2 x 1} = C'(-1, 1/2)

Soal nomor 10

Ya.

Soal nomor 11

Gambar Hasil Refleksi Terhadap Garis Refleksi l

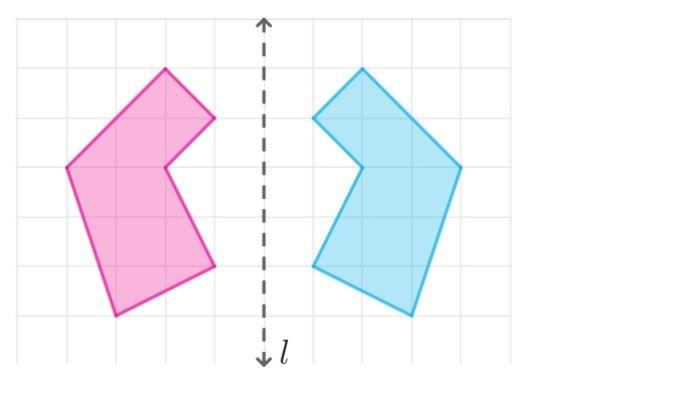
Soal nomor 12

Gambar Hasil Rotasi Titik Pusat O Sebesar 180°

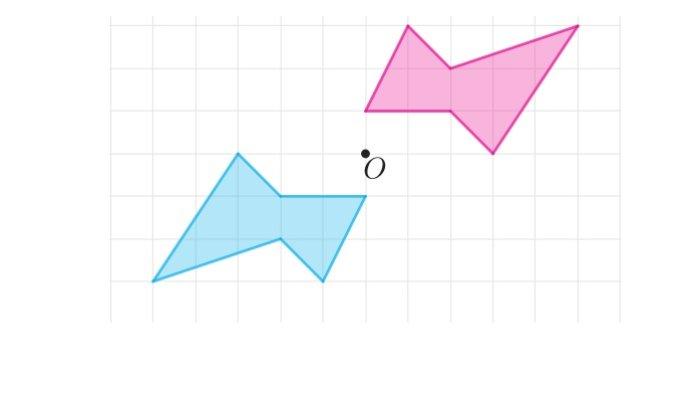
Soal nomor 13

Gambar Hasil Translasi Segi Empat

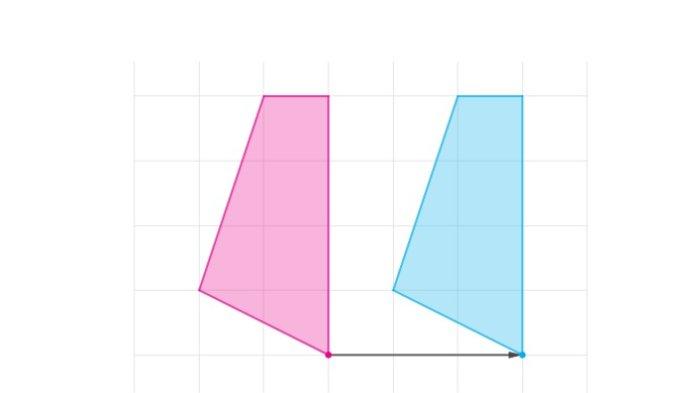
Soal nomor 14

Translasi (3|0)

Gambar Transformasi (x,y)→ (x+3,y)

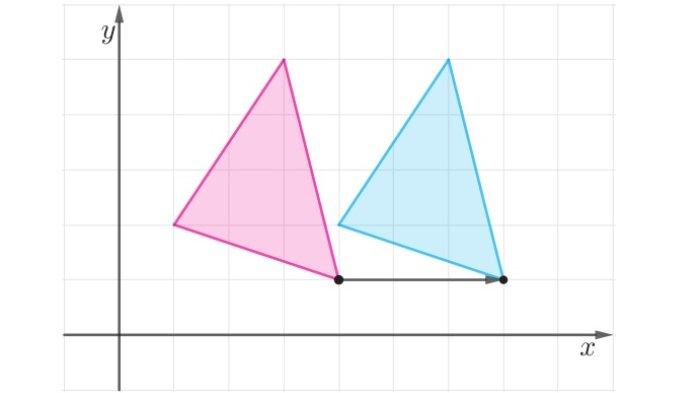
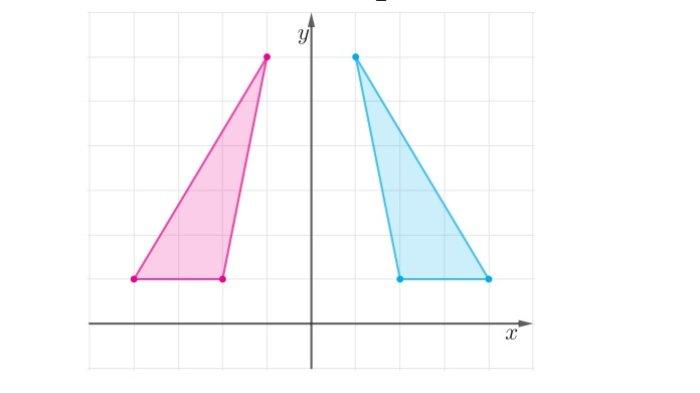
Soal nomor 15

Refleksi terhadap sumbu y

Gambar Transformasi (x,y)→ (-x,y)

Soal nomor 16

180°

Soal nomor 17

A'(3,4)

Soal nomor 18

(-y, x)

Soal nomor 19

P'(3,2)

Soal nomor 20

3x+y=-6

Soal nomor 21

M(5,4)

Soal nomor 22

1

Soal nomor 23

Gambar Permainan Golf I

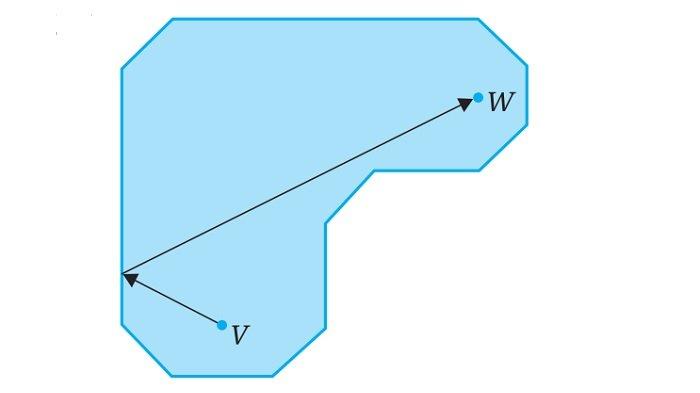
Soal nomor 24

Gambar Permainan Golf II

Soal nomor 25

Gambar Menemukan Persimpangan Terdekat

Soal nomor 26

Untuk menunjukkan bahwa AC=BC+DE, kita perhatikan dua pasang segitiga yaitu ∆DBC dengan ∆DEC dan ∆ABC dengan ∆AED.

Perhatikan bahwa ∆DBC kongruen dengan ∆DEC, karena terdapat satu sisi bersesuaian yang sama panjang yaitu DC dan dua sudut bersesuaian sama besar yaitu ∠DBC=∠DEC dan ∠BCD=∠ECD (CD garis bagi).

Sehingga EC=BC. Sedangkan ∆ABC dan ∆AED sebangun, karena terdapat 2 sudut yang sama besar yaitu∠BAC=∠EAD dan ∠ABC=∠AED.

Dan karena AB=BC, maka AE=DE.  Dengan demikian:

AC = EC + AE

AC = BC + DE

Terbukti.

Keterangan: (^) Berarti Pangkat, (/) berarti per atau se-per

Demikian kunci jawaban Matematika Kelas 9 SMP Kurikulum Merdeka halaman 204 205 206 207 209, kegiatan siswa Uji Kompetensi sesuai dengan buku Matematika edisi tahun 2022.

Disclaimer

Kunci jawaban diatas bersifat alternatif jawaban sehingga para siswa bisa memberikan eksplorasi jawaban lain.

Kunci jawaban soal diatas bisa saja berbeda sesuai dengan pemahaman tenaga pengajar atau murid. (*)