Kunci Jawaban
Kunci Jawaban Matematika Kelas 7 Semester 2 Uji Kompetisi 8 Halaman 295 296 297 298
Berikut adalah kunci jawaban matematika kelas 7 SMP semester 2 Uji Kompetensi 8 bagian soal uraian halaman 295, 296, 297, dan 298.
x = 10
Maka panjang KM = x = 10 cm ; ML dan KL = 2x-5 = 2(10) - 5 = 20 - 5 = 15 cm
4. Keliling segi-4 PQRS pada gambar di bawah adalah 22 cm.
a. Tentukan panjang PQ, SR, PS dan RQ!
b. Bagaimanakah caramu menghitung luas PQRS?
c. Berapakah luas PQRS?
Jawaban:
a. Berdasarkan kotak kecil yang panjangnya 1cm, maka :
PQ = 9 cm
SR = 3 cm
SP + RQ = 22 - PQ - SR
= 22 - 9 - 3
= 10
Karena SP sama dengan RQ maka masing, masing adalah 5cm,
SP = 5 cm
RQ = 5 cm
b. Cara menghitung luas PQRS menggunakan rumus luas trapesium,
Luas trapesium PQRS = 1/2 x jumlah sisi sejajar x tinggi
c. Luas = 1/2 x (PQ + SR) x t
= 1/2 x (9 + 3) x t
= 24 cm2
Baca juga: Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 272 273: Hitung Keliling dan Luas Segitiga
5. Diketahui bangun-bangun seperti berikut.
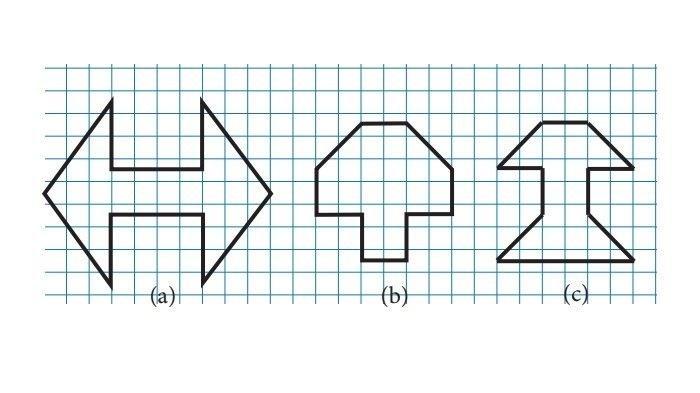
a. Tentukan luas dari tiap-tiap bangun di atas.
b. Bangun manakah yang mempunyai luas terbesar?
Jawaban:
a. Luas bangun (a) = (2 x luas segitiga) + luas persegi panjang
= (2 x 1/2 x a x t) + (p x l)
= (2 x 1/2 x 8 x 3) + (4 x 2)
= 24 + 8
= 32 satuan luas
Luas bangun (b) = (2 x luas trapesium) + luas persegi panjang
= (2 x 1/2 x (a+b) x t) + (p x l)
= (2 x 1/2 x (2 + 4) x 2) + (6 x 2)
= 12 + 12
= 24 satuan luas
Luas bangun (c) = (2 x luas trapesium) + luas persegi
= (2 x 1/2 x (a + b) x t) + (s x s)
= (2 x 1/2 x (2 + 6) x 2) + (2 x 2)
= 16 + 4
= 20 satuan luas
b. Bangun yang memiliki luas terbesar adalah bangun (a) dengan total luas 32 satuan luas.
6. Perhatikan gambar berikut.
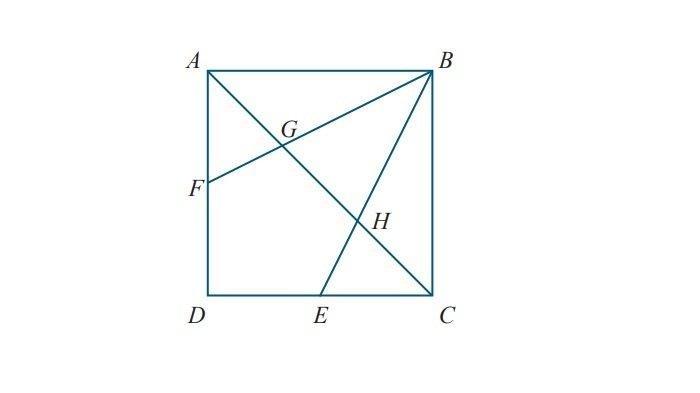
ABCD persegi dengan panjang sisi-sisinya adalah 2 cm. E adalah titik tengah CD dan F adalah titik tengah AD. Luas daerah EDFGH adalah ... cm2.
Jawaban:
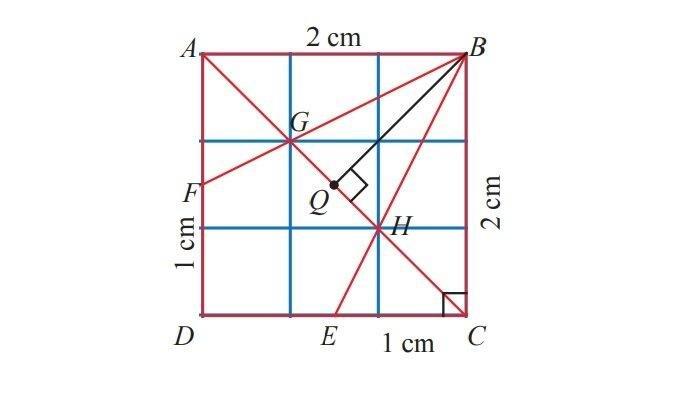
Luas daerah EDFGH = Luas persegi ABCD – (2 x Luas BCE) – Luas ΔBHG.
= 4/3 cm2
Jadi, luas EDFGH adalah 4/3 cm2.
Baca juga: Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 270 271: Hitung Keliling dan Luas Segitiga
7. Perhatikan gambar di bawah. Terdapat 4 buah layang-layang kongruen yang termuat pada persegi dan ternyata masih tersisa daerah persegi yang diarsir. Jika panjang p = 3 2 cm, dan q = 5 2 cm, maka luas daerah yang diarsir adalah …. cm2 (OSP SMP 2009)
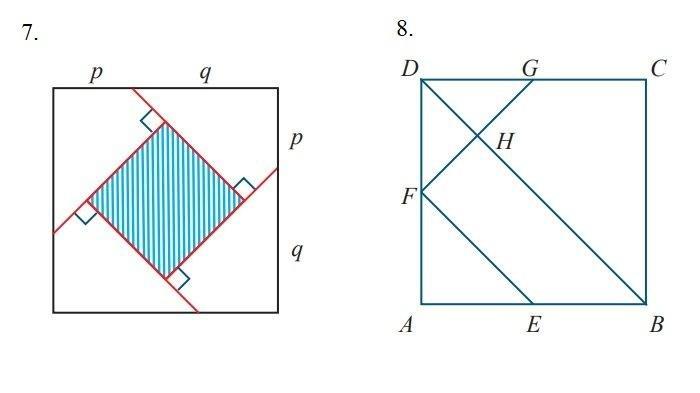
Jawaban:
Carilah panjang p + q, luas persegi besar, luas segitiga ABC
Luas daerah yang diarsir = Luas persegi – 8 Luas segitiga ABC
Jadi, luas daerah yang diarsir adalah 8 cm2.
8. Diketahui luas persegi ABCD adalah 25 m2. Jika E, F, dan G masingmasing adalah titik tengah AB, AD, dan CD seperti pada gambar berikut, maka luas trapesium BHFE adalah .... m2.
(OSP SMP 2011)
Jawaban:
Carilah panjang AE, BE, AF, FD, DG, dan GC, selanjutnya dapatkan luas trapesium BHFE:
Luas Trapesium BHFE = Luas ΔABD – Luas ΔAEF – Luas ΔDFH Jadi, luas daerah yang diarsir adalah 7,8125 cm2.
9. PATIO/ Ember terbuka di belakang rumah Nick ingin membuat patio terbuka di belakang rumah barunya. Panjang Patio adalah 5, 25 meter dan lebarnya 3 meter. Ia memerlukan 81 buah batu bata per m2.
Hitunglah berapa banyak batu bata yang diperlukan Nick untuk membuat pationya itu!
Jawaban:
Luas Patio = p x l
= 5,25 x 3
= 15,75 m2
Banyak batu = Luas / 1 x 81
= 15,75 /1 x 81
= 1275,75 batu
Jadi, banyak batu bata yang diperlukan untuk membuat patio adalah 1275,75 batu bata.
Baca juga: Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 254 255 256 257: Jenis dan Sifat Segitiga
10. Perhatikan gambar sebuah jajargenjang berikut
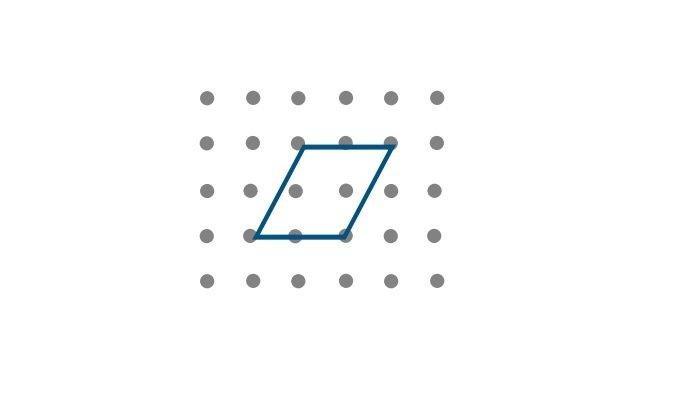
Pada kotak jawaban, buatlah minimal 4 segiempat lain yang berbeda dan memiliki luas yang sama dengan luas jajargenjang yang ditunjukkan pada gambar di atas.
(Catatan: Dua segiempat atau lebih disebut sama jika segiempat yang satu merupakan hasil pencerminan atau perputaran bangun yang lain)
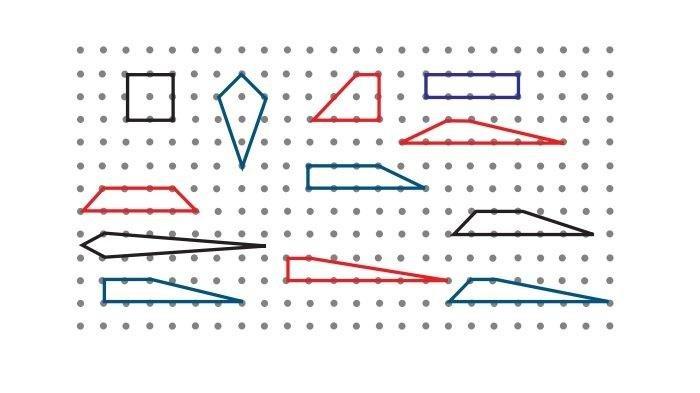
Jawaban:
Luas jajar genjang tersebut adalah, 4 satuan luas. Oleh karena itu kita mencari bangun lain yang memiliki luas yang sama dengan jajargenjang tersebut.
*) Disclaimer:
- Artikel ini hanya ditujukan kepada orang tua untuk memandu proses belajar anak.
- Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa. (*)
Artikel ini telah tayang di Tribunnews.com dengan judul Kunci Jawaban Matematika Kelas 7 Halaman 295 296, Uji Kompetensi 8: Soal Uraian dan Kunci Jawaban Matematika Kelas 7 Halaman 297 dan 298 Semester 2, Uji Kompetensi 8: Soal Uraian.
kunci jawaban
matematika
semester 2
Kurikulum 2013
Uji Kompetensi 8
Kunci Jawaban Matematika Kelas 7 Halaman 295
Kunci Jawaban Matematika Kelas 7 Halaman 296
Kunci Jawaban Matematika Kelas 7 Halaman 297
Kunci Jawaban Matematika Kelas 7 Halaman 298
| Jawaban Eksplorasi 1.3, Kunci Jawaban Matematika Kelas 5 Halaman 15 16 Kurikulum Merdeka |

|
|---|
| Jawaban Ayo Berlatih, Kunci Jawaban Matematika Kelas 5 Halaman 14 15 Kurikulum Merdeka |

|
|---|
| Jawaban Ayo Berlatih, Kunci Jawaban Matematika Kelas 5 Halaman 8 9 Kurikulum Merdeka |

|
|---|
| Jawaban Ayo Berpikir Kritis, Kunci Jawaban Matematika Kelas 5 Halaman 7 Kurikulum Merdeka |

|
|---|
| Kunci Jawaban Agama Hindu Kelas 8 Halaman 57 Kurikulum Merdeka, Asesmen Bab 2 |

|
|---|














Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.