Kunci Jawaban
Kunci Jawaban Matematika Kelas 11 Halaman 29 30 31, Kurikulum Merdeka: Sifat Komutatif dan Asosiatif
Berikut kunci Jawaban dan pembahasan soal mapel matematika kelas 11 SMA halaman 29 30 31 Kurikulum Merdeka.
Eksplorasi dilakukan untuk mengecek apakah operasi komposisi fungsi memenuhi sifat asosiatif.
Perhatikan kembali tiga fungsi di bawah ini, yaitu f, g dan h:
f(x) = 2x + 1, g(x) = x2 + 4 dan h (x) = 1/(x+1)
1. Selidikilah apakah operasi asosiatif secara umum berlaku untuk komposisi fungsi, dengan kata lain cek apakah persamaan-persamaan berikut benar:
• (f (h ◦ g)) (x) = ((f ◦ h) ◦ g)(x)?
• (h (f ◦ g)) (x) = ((h ◦ f) ◦ g)(x)?
• (g (f ◦ h)) (x) = ((g ◦ f) ◦ h)(x)?
2. Pikirkan konfigurasi komposisi lain yang mungkin dari ketiga fungsi di atas.
Cek apakah sifat asosiatif masih terpenuhi.
Baca juga: Kunci Jawaban Agama Hindu Kelas 6 Halaman 27 28 29 30, Pengertian Karmaphala
Kunci Jawaban Matematika Kelas 11 Halaman 30
1.
a. f(h ◦ g)) (x) = 2/x2 + 5 +4 = ((f ◦ h) ◦ g) (x) (Asosiatif)
b. (h(f ◦ g)) (x) = 1/2x2+ 10 = ((h ◦ f) ◦ g) (x) (Asosiatif)
c. (g(f ◦ h)) (x) = (2/x+1 +1)2 + 4 = ((g ◦ f) ◦ h) (x) (Asosiatif)
2. Konfigurasi komposisi yang mungkin:
- (f(g ◦ h)) (x) = ((f ◦ g) ◦ h) (x) (Asosiatif)
- (h(g ◦ f)) (x) = ((h ◦ g) ◦ f) (x) (Asosiatif)
Berdasarkan Eksplorasi 1.5 ternyata komposisi fungsi memenuhi sifat asosiatif.
Kunci Jawaban Matematika Kelas 11 Halaman 31
1. Jika f(x) = 1/x dan g (x) = 2x +1, tentukan
a. (f ◦ g) (x)
b. (f ◦ g)(3) dan (f ◦ g)(ꟷ3)
c. f(a) jika (f ◦ g)(a) = ꟷ1.
Jawab:
a. (f ◦ g) (x)
b. (f ◦ g)(3) dan (f ◦ g)(ꟷ3) = ꟷ1/5
c. a = ꟷ1
2. Jika f(x0 = 1/(2x+1) dan g(x) = 2x2 + 1, tentukan
a. (f ◦ g) (x)
b. (g ◦ f) (x)
c. domain dan range dari (f ◦ g) (x)
d. domain dan range dari (g ◦ f) (x)
Jawab:
Jika f(x) = 1/2x+1 dan g(x) = 2x2 + 1 maka
a. (f ◦ g) (x) = 1/4x2+3
b. (g ◦ f)(x) = 2/4x2+4x+1
c. Domain dan Range (f ◦ g)(x) adalah semua bilangan riil,
d. Domain (g ◦ f)(x) adalah semua bilang riil kecuali ꟷ1/2, Rangenya ialah semua bilangan riil.
3. Jika f(x) = 6x - 5 dan g(x) = ax + b, tentukan a dan b sehingga (f ◦ g) (x) = (g ◦ f) (x)
Jawab:
Ada banyak kemungkinan untuk nilai a dan b yang memenuhi, contoh a = ꟷ1 dan b = 2.
4. Hasil dari (f ◦ g)(x) = (2x+3)3 sedangkan f(x) = x^3 tentukan g(x).
Jawab: g(x) = 2x+3
5. Lengkapi tabel di bawah ini!
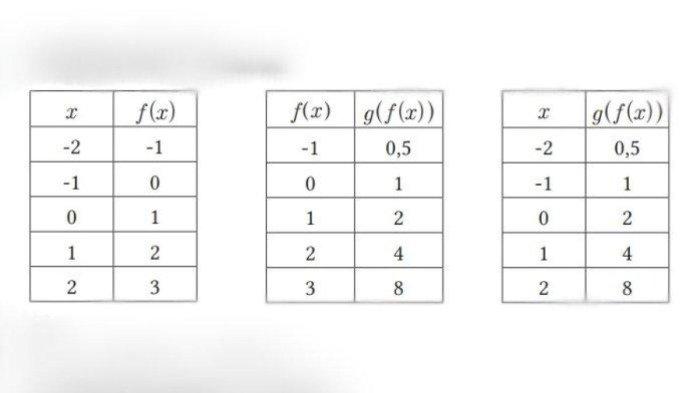
6. Jika f (3) = 7, g (3) = 6, f (6) = 13, g (6) = 12, tentukan (f ◦ g) (3).
Jawab: 13
7. Jumlah kertas yang diperlukan untuk mencetak x eksemplar modul matematika dinyatakan dalam fungsi k(x) = 250(x + 1) lembar.
Biaya pencetakan yang diperlukan untuk k lembar adalah b(k) = 400k + 20.000 (dalam rupiah).
Jika pengeluaran hari ini untuk mencetak x eksemplar modul adalah Rp10.120.000,00 tentukan banyak eksemplar modul yang dicetak.
Jawab:
b( x ) = 100.000 x + 120.000
10.120.000 = 100.000 x + 120.000
10.000.000 = 100.000 x
x = 100
8. Suatu pabrik memberikan ketentuan mengenai jumlah produksi dan jenisnya.
Produksi telepon genggam berbasis android adalah dua kali produksi telepon genggam berbasis bukan android sedangkan produksi laptop adalah tiga kali produksi telepon genggam berbasis android.
a. Gunakan mesin fungsi untuk menyatakan fungsinya.
b. Jika diproduksi 2.000 telepon genggam tidak berbasis android, berapa banyak laptop yang dihasilkan? Selesaikan dengan mesin fungsi.
Jawab:
Misal f (x) = 2x menyatakan jumlah produksi HP android dengan x menyatakan jumlah produksi HP bukan android.
Misal juga g(x) = 3x menyatakan jumlah produksi Laptop dengan x menyatakan jumlah produksi HP android.
Mesin fungsi untuk mengetahui jumlah produksi laptop jika diketahui jumlah produksi HP bukan android, siswa bisa membuat mesin fungsi:
9. Anton membeli sebuah meja belajar dari sebuah toko. Ada banyak pilihan meja dengan harga-harga yang bervariasi. Meja-meja tersebut berukuran besar.
Karena ukuran mobil Anton kecil, maka Anton memutuskan untuk menyewa jasa antar dari toko tersebut.
Setelah berdiskusi dengan pihak toko, maka total biaya yang harus dibayar adalah harga meja belajar, pajak pembelian, dan biaya angkut.
Pajak pembelian sebesar 7,5 persen harga meja. Biaya angkut sebesar Rp20.000,00.
a. Tuliskan fungsi t(x) sebagai total harga meja yang mencakup harga meja dan pajak, dengan x adalah harga satu meja.
b. Tuliskan juga fungsi f(x) sebagai total biaya yang mencakup harga meja dan biaya angkut.
c. Tuliskan kedua komposisi fungsi berikut (f ◦ t)(x) dan (t ◦ f)(x).
Manakah dari kedua fungsi yang memberikan biaya yang lebih kecil untuk setiap harga meja?
d. Peraturan daerah di tempat Anton tinggal tidak melegalkan pengenaan pajak pada biaya angkut.
Komposisi fungsi yang mana dari bagian c yang sejalan dengan perda ini?
Jawab:
Jawaban diberikan secara berurutan:
a. t (x) = x + 0,075 x
b. f (x) = x + 20000
c. (f ◦ t)(x) = x + 0,075 x + 20000 dan
d. (t ◦ f)(x) = x + 0,075 x + 1500.
Fungsi (t ◦ f)(x) (menunjukkan biaya yang lebih kecil dibandingnak (f ◦ t)(x).
e. (f ◦ t)(x)
Disclaimer:
Itu dia kunci jawaban dan soal ulasan matematika kelas 11.
Pembahasan dan kunci jawaban ini hanya digunakan sebagai panduan belajar siswa.
Siswa diharapkan untuk mengerjakan soal terlebih dahulu secara mandiri.
Kunci Jawaban Matematika Kelas 11 Halaman 29
Kunci Jawaban Matematika Kelas 11 Halaman 30
Kunci Jawaban Matematika Kelas 11 Halaman 31
kunci
Jawaban
pembahasan soal
Kurikulum Merdeka
kelas 11
matematika
| Jawaban Lembar Aktivitas 22, Kunci Jawaban IPS Kelas 8 Halaman 204 Kurikulum Merdeka |

|
|---|
| Jawaban Lembar Aktivitas 20, Kunci Jawaban IPS Kelas 8 Halaman 200 Kurikulum Merdeka |

|
|---|
| Jawaban Lembar Aktivitas 18, Kunci Jawaban IPS Kelas 8 Halaman 198 Kurikulum Merdeka |

|
|---|
| Jawaban Lembar Aktivitas 17, Kunci Jawaban IPS Kelas 8 Halaman 194 195 Kurikulum Merdeka |

|
|---|
| Jawaban Aktivitas 1, Kunci Jawaban PAI Kelas 9 Halaman 149 Kurikulum Merdeka |

|
|---|














Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.