Kunci Jawaban
Kunci Jawaban Matematika Kelas 12 Halaman 25 26, BAB 1: Menghitung Panjang Rusuk Kubus
Berikut kunci Jawaban dan pembahasan soal mapel matematika kelas 12 SMA halaman 25 26 BAB 1.
10. Panjang rusuk kubus ABCD.EFGH adalah 6 cm. Tentukan jarak titik C dengan bidang BDG.
Alternatif Penyelesaian:
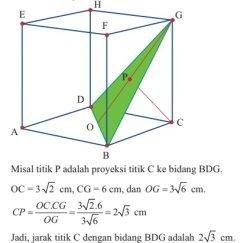
Kunci Jawaban Matematika Kelas 12 Halaman 26
6. Dalam kubus ABCD.EFGH titik S adalah titik tengah sisi CD dan P adalah titik tengah diagonal ruang BH. Tentukan perbandingan volum limas P.BCS dan volum kubus ABCD.EFGH.
Jawaban:
Cari terlebih dahulu volume limas P.BCS
Volume limas P.BCS:
= 1/3 x Luas alas x t
= 1/3 x 1/2 x BC x SC x 1/2a
= 1/3 x 1/2 x a x 12a x 1/2a
= 1/24a3
Cari volume kubus ABCD.EFGH
Diketahui perbandingan volume limas P.BCS dan volume kubus ABCD.EFGH adalah:
= 1/24a3 : a3
= 1/24 : 1
= 1 : 24
7. Diketahui kubus ABCD.EFGH dengan panjang rusuk a cm. S merupakan proyeksi titik C pada bidang AFH.Tentukan jarak titik A ke titik S.
Jawaban:
Diketahui dari segitiga ACP maka:
AP = CP = 1/2 a√6 (diperoleh phytagoras AE dan EP)
AC = a√2 (diagonal sisi)
PQ = a (rusuk kubus)
Dengan saling tegak lurus, maka berlaku aturan luas pada segitiga yakni:
AC x PQ = AP x CS
CS = AC x PQ/AP
CS = a√2 x a / (1/2a√6)
CS = 2a√2 /√6
CS = 2a/√3
CS = 2/3 a√3
Dan juga berlaku phytagoras sebagai berikut:
AS2 = AC2 -CS2
AS2 = (a√2)2 - (2/3 a√3)2
AS2 = 2a2 - 4/3a2
AS2 = 2/3 a2
AS = √(2/3a2)
AS = a√2 / √3
Dengan rasionalisasi:
AS = 1/3 a√6 cm
Baca juga: Kunci Jawaban Fisika Kelas 11 Halaman 65 66 67 68 70, Latihan 2.2: Panjang Garis Singgung
Kunci Jawaban Matematika Kelas 12 Halaman 25
Kunci Jawaban Matematika Kelas 12 Halaman 26
kunci
Jawaban
pembahasan soal
matematika
kelas 12
| Jawaban Eksplorasi 1.3, Kunci Jawaban Matematika Kelas 5 Halaman 15 16 Kurikulum Merdeka |

|
|---|
| Jawaban Ayo Berlatih, Kunci Jawaban Matematika Kelas 5 Halaman 14 15 Kurikulum Merdeka |

|
|---|
| Jawaban Ayo Berlatih, Kunci Jawaban Matematika Kelas 5 Halaman 8 9 Kurikulum Merdeka |

|
|---|
| Jawaban Ayo Berpikir Kritis, Kunci Jawaban Matematika Kelas 5 Halaman 7 Kurikulum Merdeka |

|
|---|
| Kunci Jawaban Agama Hindu Kelas 8 Halaman 57 Kurikulum Merdeka, Asesmen Bab 2 |

|
|---|













Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.